
从三角级数到傅里叶级数
傅里叶级数在信号处理、概率论、统计学、密码学、声学、光学等领域都有着广泛的应用。它是指任意的一个分段连续并有分段连续的一阶和二阶导数的周期函数,能够用一个无穷的”傅里叶级数“来表示。
非周期函数的傅里叶展开式
本文详细介绍了傅里叶系数的计算方法,并对非周期函数进行延拓,将一个相关的分段周期函数展开为傅里叶级数。展现了傅里叶积分的计算过程和如何无限逼近原函数。
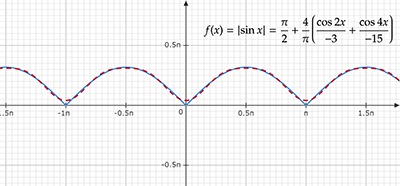
周期函数的傅里叶展开式
本篇主要介绍周期函数的傅里叶展开式,如果函数不以2π为周期,需要假定以2π为周期进行延拓,以2π为周期的连续函数在使用傅里叶展开时,即使较少的项也有很好的逼近效果。
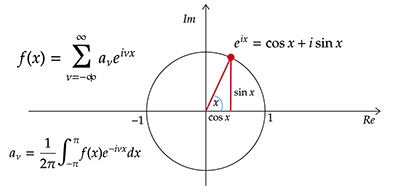
傅立叶级数的复形式
通过欧拉公式提供复点至极坐标的变换,使用复平面来分析三角级数必须引入复数,本文主要说明使用欧拉公式来表示傅里叶的复数形式,欧拉公式在数学、物理和工程领域应用广泛。
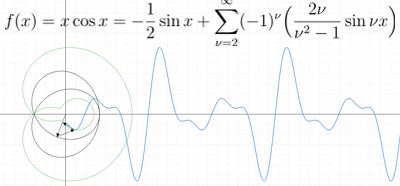
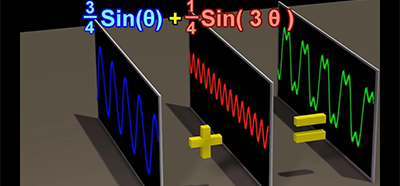
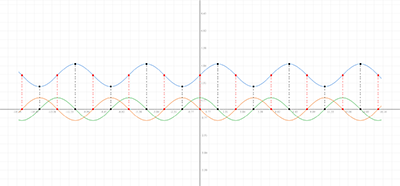
傅里叶级数的可视化
对一个函数进行傅里叶展开后,借助函数图像的可视化可对傅里叶展开式进行验证,通过不断增加傅里叶多项式的阶数在函数图像上能感受到不断逼近原函数的过程,傅里叶级数的可视化可应用于数字信号的处理。
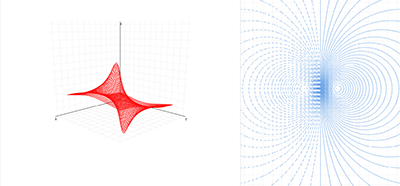
二元函数的等高线算法
二元函数的等高线相当于用平行于xy的平面来切割曲面得到的曲线,并把相交的曲线垂直投射到xy平面后获得的曲线。Marching Squares算法可以计算等高线。等高线靠的很近的地方,说明函数上升下降很陡;分得很开的地方,说明是平坦的。
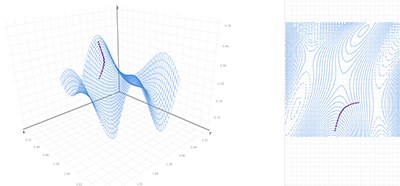
方向导数和梯度
梯度下降(Gradient descent)是机器学习中最常用的计算代价函数的方法,它是一个一阶最佳化算法,使用梯度算法可以找到一个函数向下或向上变化最快的方向,从而获取函数的局部极值。
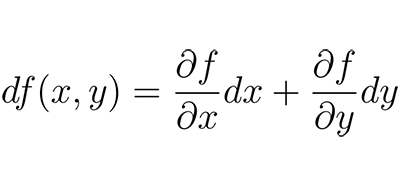
全微分用于近似值计算和误差估计
在微积分中,函数在某点的全微分(total derivative)是指该函数在该点附近关于其自变量的最佳线性近似,与偏微分不同,全微分反映了函数关于其所有自变量的线性性近似,而非单个自变量。可用于复杂函数近似值的计算和误差估计。

复合函数的偏导数
为了求出复合函数的偏导数,我们必须首先求出复合函数关于每一个变量的导数,再把这个导数中的每一个乘以对应变量关于对应函数的导数,并将所有的乘积相加。
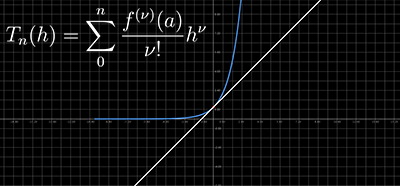
用泰勒多项式近似表达函数
泰勒定理描述了一个可微函数,如果函数足够光滑的话,在已知函数在某一点的各阶导数值的情况之下,泰勒公式可以用这些导数值做系数构建一个多项式来近似函数在这一点的临域中的值,这个多项式成为泰勒多项式。
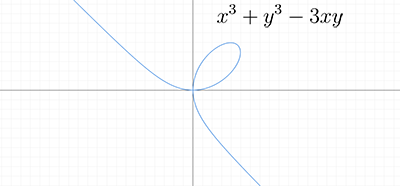
四叉树算法和隐函数图像
含有两个或两个以上自变量的函数中,隐函数无法显式地表示为y=f(x)的形式,因此无法像显函数那样通过指定x值计算出对应的y值在平面直角坐标系上建立映射。四叉树算法可以克服传统算法的缺点准确地建立隐函数的图像。
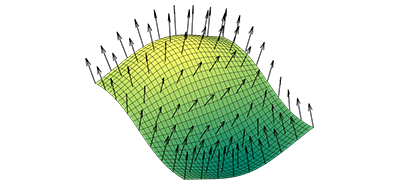
向量的运算以及法线
三维平面的法线是垂直于该平面的三维向量。曲面在某点处的法线为垂直于该点切平面的向量。在计算机图形领域,法线決定着曲面与光源的浓淡处理,对于每个点光源位置,其亮度取决于曲面法线的方向。
曲线的凹凸性与拐点
拐点(Inflection point)或称反曲点,是一条连续曲线由凸转凹,或由凹转凸的点,或者说,是使切线穿越曲线的点。若函数在拐点有二阶导数,则二阶导数必为零或不存在。在现实生活中通常指事物的发展趋势开始改变的地方。

三元隐函数与空间曲面
三元隐函数的图形表现为空间中的曲面,它与显函数不同,无法通过z=f(x,y)的形式直接计算函数的值然后在空间中建立映射。该文章介绍了通过在空间中构造立方体的形式使用线性插值近似计算曲面的顶点,然后将这些顶点连接成曲面。
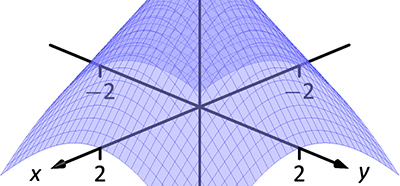
函数的极值和最值
函数的极值是要一个局部概念,最值是一个全局概念。极值和最值都需要通过计算函数的导函或偏导数来求得。在二元函数中,使得偏导数为零的点叫极值点、稳定点或临界点。 在科学和生产实践中存在着许多和极值有关的问题。

在Qt中编译Qklabs
Qklabs项目通过Qt C++结合OpenGL实现了数学一些常用的算法以及数学图像可视化,可作为用户学习高等数学和算法的实验工具。本文介绍了如何使用Qt C++编译Qklabs。
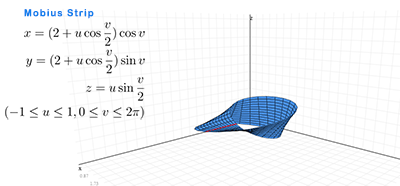
参数方程和空间曲面
通过显式或隐式函数来表示空间曲面受到诸多限制。受特定算法的影响,使用隐函数绘制空间曲面也无法做到面面俱到。本文分析了常用曲面参数方程推导过程以及如何在OpenGL中绘制空间参数曲面,帮助用户了解三维空间中参数曲面和空间解析几何算法的实现。
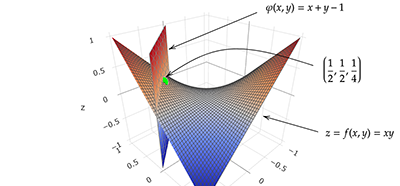
拉格朗日乘数法与条件极值
通过显式或隐式函数来表示空间曲面受到诸多限制。受特定算法的影响,使用隐函数绘制空间曲面也无法做到面面俱到。本文分析了常用曲面参数方程推导过程以及如何在OpenGL中绘制空间参数曲面,帮助用户了解三维空间中参数曲面和空间解析几何算法的实现。
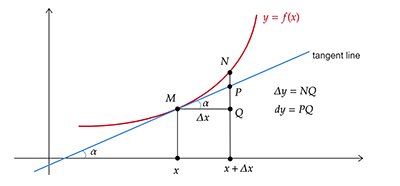
函数的微分
函数的微分是指对函数的局部变化的一种线性描述。微分可以近似地描述当函数自变量的取值作足够小的改变时,函数的值是怎样改变的。微分主要用于线性函数的改变量,这是微积分的基本概念之一。
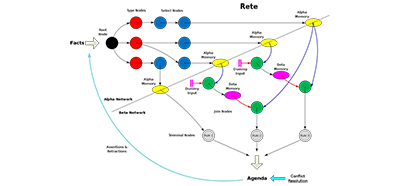
Rete算法和逻辑推理
Rete 算法是一种用于处理规则引擎和专家系统中的规则匹配和推理的算法。主要目的是加速规则系统对大规模数据集进行规则匹配和条件测试。它使用网络结构来表示规则,通过对输入数据进行逐步匹配来确定哪些规则被触发。
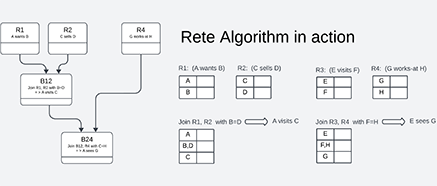
Rete算法运行时推理
在运行时,Rete算法将事实集合与构建的网络进行匹配。它递归地遍历网络,查找匹配每个规则的条件。当一个条件匹配时,Rete算法将匹配的事实传递给该条件的下一个条件,直到匹配整个规则。