函数的极值和最值
发布于 2023/07/23 更新于 2023/07/23
作者 趣宽科技 码云上的源文件
码云上的源文件
- 极值是局部概念。
- 极值必须在定义域内部取得
- 极值必须是定义域的内点
- 定义域的边界点不可能是极值点
如函数
$$
z=\sqrt{a^2-x^2-y^2}
$$
它的图像是一个半球面:
当\(x=0, y=0\)时,函数取得极大值,也是最大值,因为它是在定义域内取得的。但是\(z=0\)时是最小值,由于自变量\(x,y\)处于函数的边界,所以不能称之为极值。
\(y=f(x)\),\(f(x_0)\)是极值,\(f’(x_0)\)存在,则\(f'(x_0)=0\)
设\(z=f(x,y)\)在\((x_0, y_0)\)处取得极值,且偏导数\(f_x(x_0,y_0), f_y(x_0, y_0)\)存在,则
$$
f_x(x_0, y_0) = 0, \quad f_y(x_0, y_0) = 0
$$
一元函数极值的必要条件是函数在该点处的导数等于零,意味该点的切线与\(x\)轴平行(\(tan=\frac{y}{x}, (y=0)\))。
设函数在\(z=f(x,y)\)在\((x_0, y_0)\)处取得极值,则\(f_x(x_0, y_0) = 0, f_y(x_0, y_0) = 0\),曲面\(z=f(x,y)\)在点\((x_0, y_0, z_0)\)处有切面:
$$
z=f(x_0, y_0) + (x-x_0)f_x(x_0, y_0) + (y-y_0)f_y(x_0, y_0) \implies z = f(x_0, y_0)
$$
所以\(z\)是水平的切平面。
驻点\((x_0, y_0)\)处函数的偏导数都等于零
$$
(x_0, y_0): f_x(x_0, y_0) = 0, f_y(x_0, y_0) = 0
$$
但驻点不一定是极值点,比如:
$$
z=f(x,y) = xy
$$
$$
\frac{\partial z}{\partial x}=y, \quad \frac{\partial z}{\partial y}=x
$$
令它们的偏导数都等于零,得到点\((0,0)\),但是该点不是函数的极值点。如下图:
不是极值点的驻点,称为鞍点(saddle point)。极值点不一定是驻点,因为它不一定有偏导数。例如:
$$
z=f(x,y) = \sqrt{x^2+y^2}
$$
它是一个圆锥面,它的极小值点在原点。但在该点无偏导数。这是因为
$$
\frac{\partial z}{\partial x}=\frac{x}{\sqrt{x^2+y^2}}
$$
等\(x=0,y=0\)时是无意义的。
$$
\
\begin{cases}
f'(x_0) = 0, \\
f''(x_0) > 0 \implies 极小值 \\
f''(x_0) < 0 \implies 极大值
\end{cases}
$$
设函数\(z=f(x,y)\)在点\((x_0, y_0)\)的某领域内连续有一阶及二阶偏导数,有\(f_x(x_0, y_0) = 0, f_y(x_0, y_0)=0\),令二阶偏导数
$$
f_{xx}(x_0, y_0) = A, \quad f_{xy}(x_0, y_0)=B, \quad f_{yy}(x_0, y_0) = C
$$
则\(f(x,y)\)在点\((x_0, y_0)\)是否取得极值的条件如下:
1.当\(AC - B^2 > 0\)时具有极值,且当\(A < 0\)时有极大值,当\(A > 0\)时有极小值。
2.当\(AC - B^2 < 0\)时没有极值。
3.当\(AC - B^2=0\)时可能有极值,也可能没有极值,还需要另作讨论。
求下列函数的极值
$$
f(x,y)=x^4+y^4-4xy
$$
$$
f_x(x,y)=4x^3-4y=0 \quad (1)
$$
$$
f_y(x,y)=4y^3-4x=0 \quad (2)
$$
解上述方程组,\(y=x^3\),代入\((2)\)得到:
$$
y^9-x = 0
$$
可得到三个驻点\((0,0), (1,1), (-1,-1)\)。
$$
A = f_{xx} = 12x^2, \quad B = f_{xy}=-4 , \quad f_{yy}=12y^2
$$
那么
$$
AC - B^2 = 144x^2y^2 - 16
$$
分别讨论三个驻点的极值。在点\((0,0)\)处:
$$
AC-B^2 = -16 < 0
$$
所以在(0,0)处没有极值,没有极值点的驻点为鞍点。在点\((1,1)\)处:
$$
AC-B^2=144-16 > 0,
$$
有极值,又因为\(A=12 > 0\),所以函数有极小值,极小值是
$$
f(1,1)=-2
$$
在点\((-1,1)\)处,由于\(AC-B^2=144-16 > 0\),,并且\(A=12 > 0\), 所以该点有极小值。
$$
f(-1,-1)=-2
$$
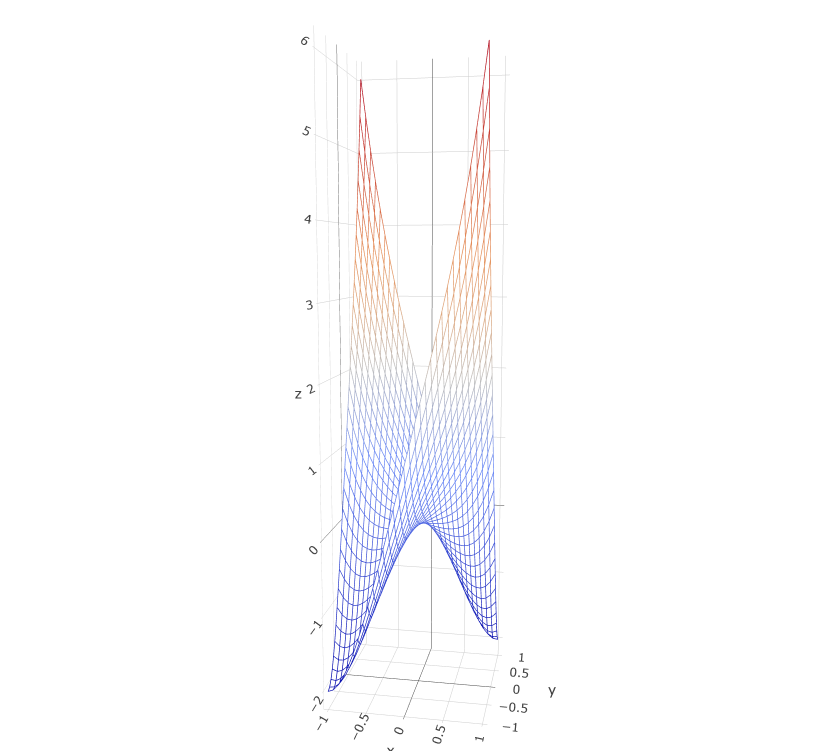
该函数图像如下:
函数\(f(x,y)\)在一区域\(D\)上的最大(最小)的函数值称为函数在该区域上的最大(最小)值,简称最值。最值是一个整体概念,相比之下,极值是一个局部概念。函数\(f(x,y)\)在一区域\(D\)上的最值可以在区域内部取到(也是极值)。也可以在边界取到(但非极值)。
- 定义域内部的极值点(包括驻点和不可导点)
- 定义域的边界点
定理:在闭界区域上的连续多元函数在该区域上必有最大函数值和最小函数值。比较一元函数的情形:闭区间上的连续函数在该区间上有最大的函数值和最小的函数值。
- 求出定义域内部可能得极值点(包括驻点(偏导数为零的点)和不可导点)
- 求出定义域的边界上可能的最值点。
- 比较上述各函数值的大小得到最大值和最小值。
由于多元函数的定义域边界有无穷多个点,因此,求多元函数的最值比较复杂。如果根据问题可以知道最值出现在定义域内部,则可避免讨论边界点。接下来讨论一个没有边界点的最值得例子。
要做一个容积为\(V\)的无盖长方形水箱,问水箱的长、宽、高各取多大,才能是用料最省?
要使用料最省,意味着用料的面积取得最小值。水箱的面积
$$
S = xy + 2(xz + yz)
$$
因为
$$
V = xyz \implies z = \frac{V}{xy}
$$
所以,目标函数
$$
S = xy + 2V (\frac{1}{y} + \frac{1}{x}) \quad (0 < x,y < +\infty)
$$
定义域是开区域,所以没有边界点,最值在区域内部取到,先求目标函数的驻点:
$$
\frac{\partial S}{\partial x} = y - \frac{2V}{x^2} = 0, \quad \frac{\partial S}{\partial y} = x - \frac{2V}{y^2} = 0
$$
解该方程组可得到驻点:
$$
(x,y)= (\sqrt[3]{2V}, \sqrt[3]{2V})
$$
根据极值计算公式,我们可以得到:
$$
A = S_{xx}=\frac{4V}{x^3} = \frac{4V}{(\sqrt[3]{2V})^3}=\frac{4V}{2V} = 2
$$
$$
B = S_{xy} = 1
$$
$$
C = S_{yy} = \frac{4V}{y^3} = \frac{4V}{(\sqrt[3]{2V})^3} = 2
$$
根据多元函数极值的定理,因为\(AC - B^2 = 3 > 0 \)所以存在极值。由于\(A = 2 > 0\),所以\(S\)在点\((x,y)= (\sqrt[3]{2V}, \sqrt[3]{2V})\)取得极小值。所以当
$$
x = \sqrt[3]{2V}, y = \sqrt[3]{2V},z=\frac{V}{xy}=\frac{\sqrt[3]{2V}}{2}
$$
时,用料最省。
有温度场
$$
T(x,y)=x^2+y^2-xy
$$
区域:\(|x|+|y| \leq 1 \),求最热和最冷点。该区域是一个正方形,如下图:
这是一个在有界闭区域上求连续函数的最值问题。
1.求定义域内部的驻点
$$
\frac{\partial T}{\partial x} = 2x - y = 0, \quad \frac{\partial T}{\partial y} = 2y - x = 0
$$
解上述方程,求得驻点\((0,0)\)
2. 求定义域边界上可能的最值点(可疑点),其次考虑四条边上可能的最值点:
在\(AB\)边上,\(y=1-x, (0 < x < 1) \),
$$
T(x,y) = x^2+y^2-xy = x^2 + (1-x)^2 - x(1-x)
$$
$$
=3x^2-3x+1
$$
$$
\frac{\partial T}{\partial x} = 6x - 3 = 0 \implies x = \frac{1}{2}, y = 1-x = \frac{1}{2}
$$
因此在\(AB\)边上可能的最值点是\(E(\frac{1}{2}, \frac{1}{2})\),类似的方法还可以求得其它各边的可疑点:
$$
F(-\frac{1}{2}, \frac{1}{2}), \quad G(-\frac{1}{2},-\frac{1}{2}), H(\frac{1}{2},-\frac{1}{2})
$$
比较9个点的值的大小。
$$
在原点处O: T = 0
$$
$$
A,B,C,D: T = 1
$$
$$
E,G: T = \frac{1}{4}
$$
$$
F,H: T = \frac{3}{4}
$$
所以最冷在原点处,最热在\(A,B,C,D\)4个点处。