用泰勒多项式近似表达函数
发布于 2023/06/01 更新于 2023/06/01
作者 趣宽科技 码云上的源文件
码云上的源文件
在数学中,泰勒公式(Taylor's Formula)是一个用函数在某点的信息描述其附近取值的公式。这个公式来自于微积分的泰勒定理,泰勒定理描述了一个可微函数,如果函数足够光滑的话,在已知函数在某一点的各阶导数值的情况之下,泰勒公式可以用这些导数值做系数构建一个多项式来近似函数在这一点的临域中的值,这个多项式成为泰勒多项式(Taylor's polynomial)。泰勒公式还给出了余项及这个多项式和实际的函数值之间的偏差。
泰勒公式的初衷是用多项式来近似地表示函数在某点周围的情况。比如说指数函数\(e^x在x=0\)的附近可以用系列多项式来近似地表示:(根据幂级数中提到到的无穷展开式要求\(|x| < 1 或 x^2 < 1 \),在这个区间之外是不成立的)
$$
e^x = 1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots++\frac{x^n}{n!} + \cdots.
$$
或
$$
e^x \approx 1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots++\frac{x^n}{n!}.
$$
称为指数函数在\(0\)处的\(n\)阶泰勒展开式。对于这类函数,当它的\(n+1\)阶导数不为\(0\)时,这个公式只对\(0\)附近的\(x\)有用。\(x\)离越远,这个公式越不准确。 实际函数值和多项式的偏差称为泰勒公式的余项。
$$
R_n(x)=e^x - (1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots++\frac{x^n}{n!}).
$$
关于\(x\)的一个\(n\)次多项式,譬如说
$$
f(x)=a_0+a_1x+a_2x^2+\cdots+a_nx^n,
$$
其泰勒表示是一个完全初等的代数式。
假设把\(x\)换成\(a+h=b,( a是坐标轴上的一点,h是距离a点的偏移)\),并按\(h\)的幂展开每一项,就可以得到一个形式为
$$
f(a+h)=c_0+c_1h+c_2h^2+\cdots+c_nh^n
$$
的表达式。泰勒公式实质上就是关于这些系数的关系式
$$
c_\nu=\frac{1}{\nu!}f^{(\nu)}(a),
$$
\(\nu=0\)时对应\(c_0\),表示函数在\(a\)点的值。系数\(\nu由f和f\)的各阶导数在\(x=a\)的值来表示。
$$
f(a+h)=f(a)+hf'(a)+\frac{h^2}{2!}f''(a)+\frac{h^3}{3!}f'''(a)+\cdots
$$
$$
+\frac{h^n}{n!}f^{(n)}(a).
$$
令\(a+h=x,那么h = x-a\),所以上述也可以写成
$$
f(x)=f(a)+(x-a)f'(a)+\frac{(x-a)^2}{2!}f''(a)+\frac{(x-a)^3}{3!}f'''(a)+\cdots
$$
$$
+\frac{(x-a)^n}{n!}f^{(n)}(a).
$$
因为n次多项式(最高幂是n)的n+1次导数是0\((f^{(n+1)})\),所以上述公式自然而然就结束了。
也可以使用下面的公式表示
$$
T_n(h)=\sum_0^n\frac{f^{(\nu)}(a)}{\nu!}h^{\nu}
$$
如果一个函数\(f(t)\)在包含点\(a和b\)的一个闭区间上直到第\(n+1\)阶连续可微,那么
$$
f(b)=f(a)+(b-a)f'(a)+\frac{f''(a)}{2!}(b-a)^2+\cdots+\frac{f^{(n)}(a)}{n!}(b-a)^n+R_{n+1},
$$
其中余项式\(R_n依赖于n,a和b,\)并由表达式
$$
R_n=\frac{1}{n!}\int_{a}^b(b-t)^nf^{(n+1)}(t)dt
$$
给出。
假设多项式
$$
f(x)=x^3+x^2+x+1
$$
求该函数在\(a=1\)处的3阶泰勒展开式,根据上述的泰勒公式可得
$$
f(x)=f(a)+f'(a)(x-a)+\frac{f''(a)}{2!}(x-a)^2+\frac{f'''(a)}{3!}(x-a)^3
$$
因为
$$
f'=3x^2+2x+1
$$
$$
f''=6x+2
$$
$$
f'''=6
$$
因此
$$
f(x)=4+6(x-1)+4(x-1)^2+(x-1)^3
$$
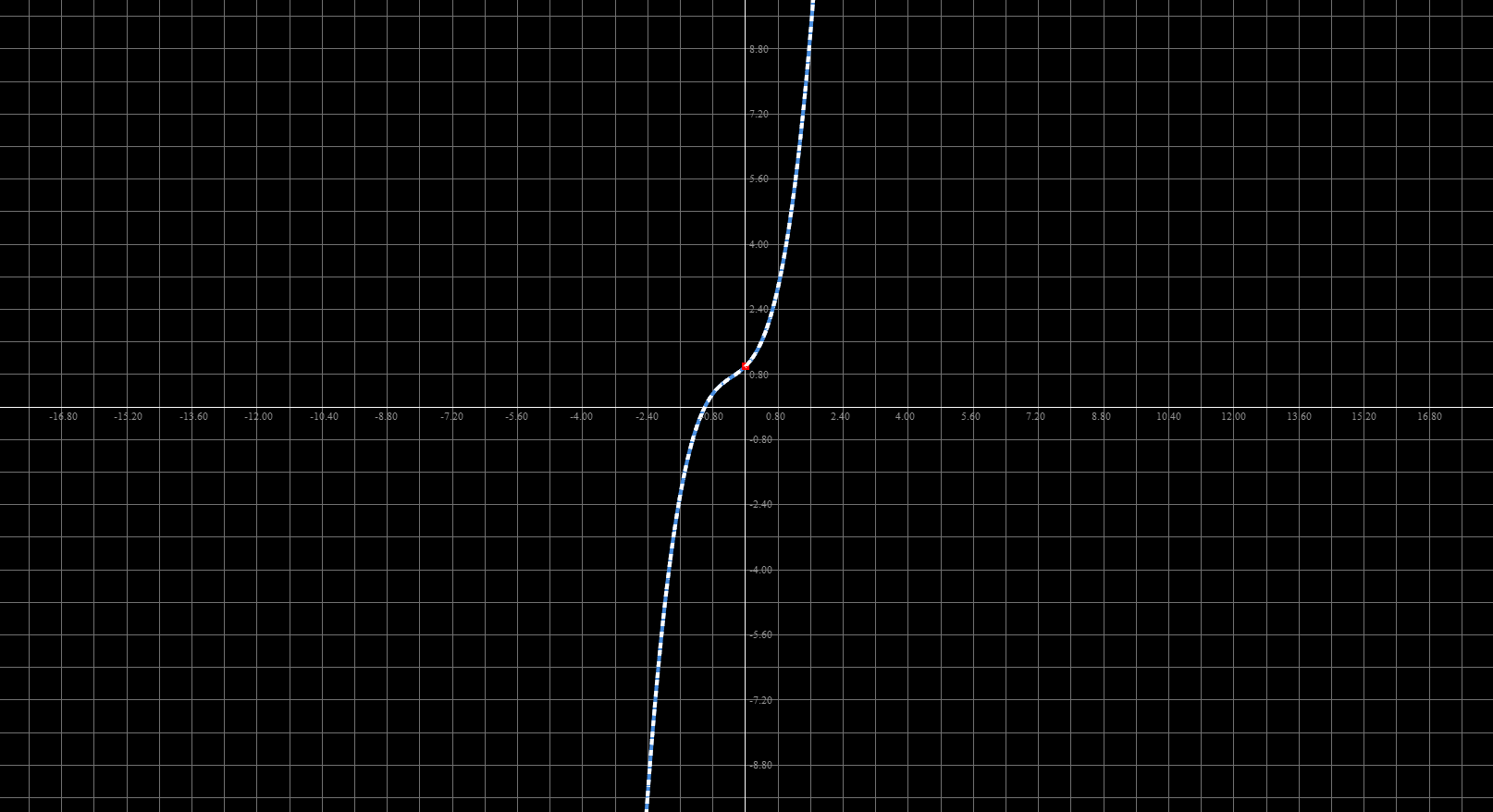
该函数的在\(a=0\)展开的泰勒多项式,当多项式数量为4(包括首项)时,可以看出基本与函数完全重合。