非周期函数的傅里叶展开式
发布于 2023/03/03 更新于 2023/03/03
作者 趣宽科技 码云上的源文件
码云上的源文件
在前一篇中,我们已经知道傅里叶级数的表达式和计算”傅里叶系数“的方法,这篇将通过一些例子来说明如何将一个相关的分段周期函数展开为傅里叶级数。
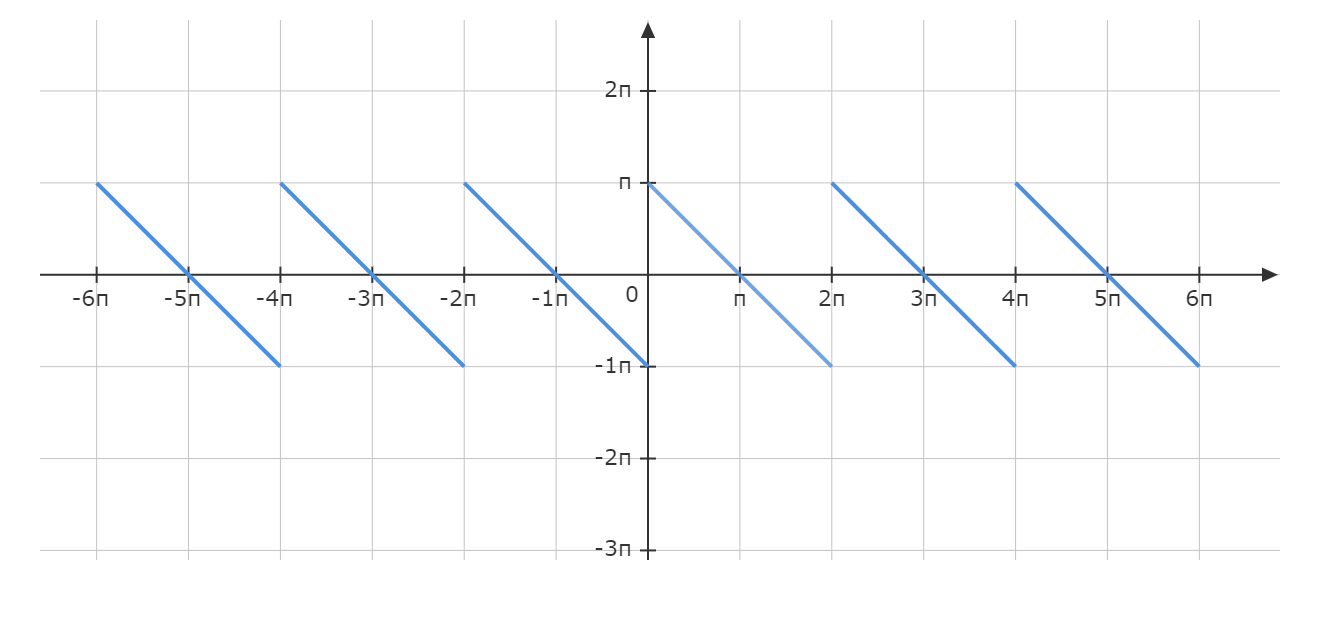
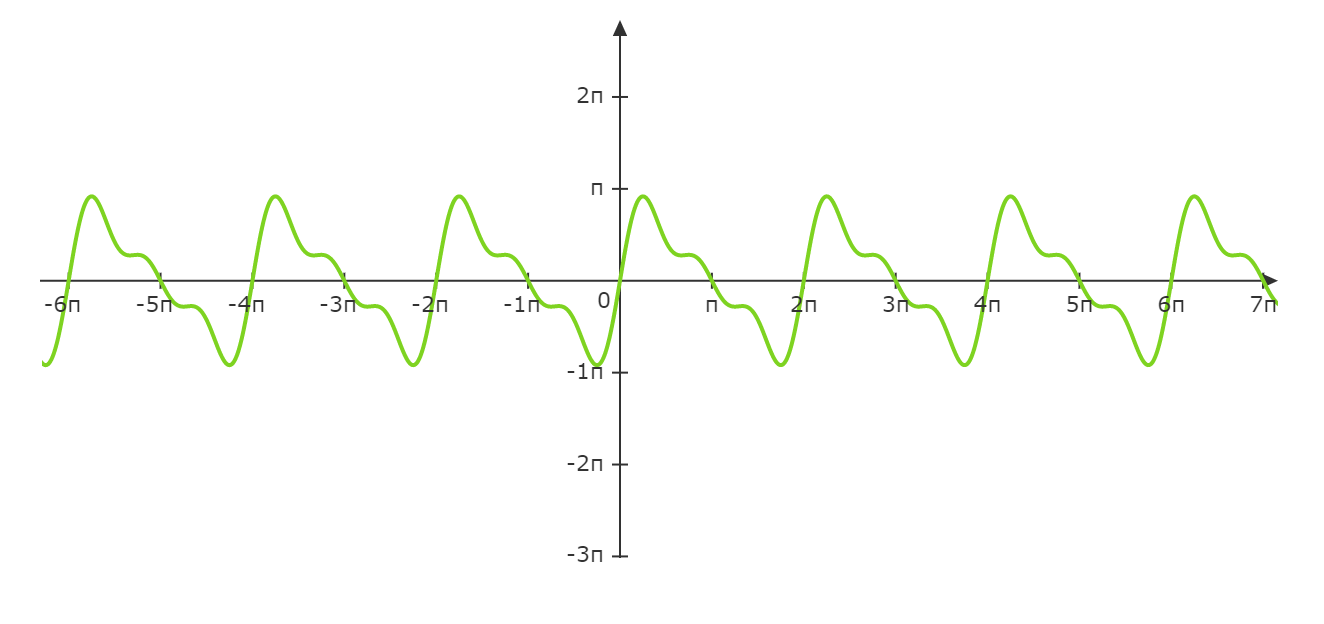
假设有一个分段周期函数,它满足: $$\ f(x) = \begin{cases} \pi -x, & \quad 当 x > 0\\ 0, & \quad 当x=0,\\ -\pi-x, & \quad 当x<0 \end{cases} $$它在区间\(-\pi < x < \pi \),将\(f(x)\)展开为傅里叶级数,该函数的图像如下: 该函数原本不是一个周期函数,现在为了使用傅里叶展开,假设它具有\(2\pi\)周期,所以对函数进行了延拓。按照函数平移的法则(左加右减)对上述函数进行延拓后是由下面的分段函数组成$$\ f(x) \begin{cases} \pi-x & 0 \leq x \leq 2\pi \\ \pi-(x-2\pi) & 2\pi \leq x \leq 4\pi \\ \pi-(x-4\pi) & 4\pi \leq x \leq 6\pi \\ -\pi-(x+2\pi) & -2\pi \leq x \leq 0 \\ -\pi-(x+4\pi) & -4\pi \leq x \leq -2\pi \\ -\pi-(x+6\pi) & -6\pi \leq x \leq -4\pi \end{cases}$$计算傅里叶系数, \(a_{\nu}\)的计算过程:$$a_{\nu}=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos \nu x dx$$$$=\frac{1}{\pi}\int_{-\pi}^{0}(-\pi-x)\cos \nu x dx + \frac{1}{\pi}\int_{0}^{\pi}(\pi-x)\cos \nu x dx$$$$=\frac{1} {\pi} \Big(\int_{-\pi}^{0}-\pi\cos \nu x dx - \int_{-\pi}^{0}x\cos \nu x dx\Big)+ \frac{1}{\pi}\Big(\int_{0}^{\pi}\pi\cos \nu x dx - \int_{0}^{\pi}x\cos \nu x dx \Big)$$$$=\frac{1}{\pi}\Big(-\frac{\pi\sin\nu \pi}{\nu} + \frac{\nu \pi \sin\nu \pi +\cos \nu \pi - 1}{\nu^2}\Big)+$$$$\frac{1}{\pi}\Big(\frac{\pi\sin\nu \pi}{\nu} - \frac{\nu \pi \sin\nu \pi +\cos \nu \pi - 1}{\nu^2}\Big)+$$$$= 0$$\(b_{\nu}\)的计算过程:$$a_{\nu}=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin \nu x dx$$$$=\frac{1}{\pi}\int_{-\pi}^{0}(-\pi-x)\sin \nu x dx + \frac{1}{\pi}\int_{0}^{\pi}(\pi-x)\sin \nu x dx$$$$=\frac{1} {\pi} \Big(\int_{-\pi}^{0}-\pi\sin \nu x dx - \int_{-\pi}^{0}x\sin \nu x dx\Big)+ \frac{1}{\pi}\Big(\int_{0}^{\pi}\pi\sin \nu x dx - \int_{0}^{\pi}x\sin \nu x dx \Big)$$$$=\frac{1}{\pi}\Big(\frac{\pi-\pi\cos\nu \pi}{\nu} - \frac{\sin\nu \pi -\nu \pi\cos\nu \pi}{\nu^2}\Big)+$$$$\frac{1}{\pi}\Big(\frac{\pi-\pi\cos\nu \pi}{\nu} - \frac{\sin\nu \pi -\nu \pi\cos\nu \pi}{\nu^2}\Big)+$$$$=\frac{2(\nu\pi - sin\nu\pi)}{\nu^2\pi }$$根据傅里叶的展开式 $$f(x)=\frac{a_0}{2}+\sum_{\nu=1}^{\infty}(a_{\nu}\cos \nu x + b_{\nu} \sin \nu x)$$可得傅里叶级数的和式:$$f(x)=\sum_{\nu=1}^{\infty}\frac{2(\nu\pi - \sin\nu\pi)}{\nu^2\pi }\sin \nu x$$$$=2\sum_{\nu=1}^{\infty}\frac{(\nu\pi - \sin\nu\pi)}{\nu^2\pi }\sin \nu x$$$$=2\sum_{\nu=1}^{\infty}\frac{\sin\nu x}{\nu}$$代入\(\nu\)项得到最终的傅里叶级数:$$f(x)=2\Big(\sin x +\frac{\sin2x}{2}+\frac{\sin3x}{3}+\cdots\Big)$$当我们取傅里叶级数的前3项时,它的函数图:
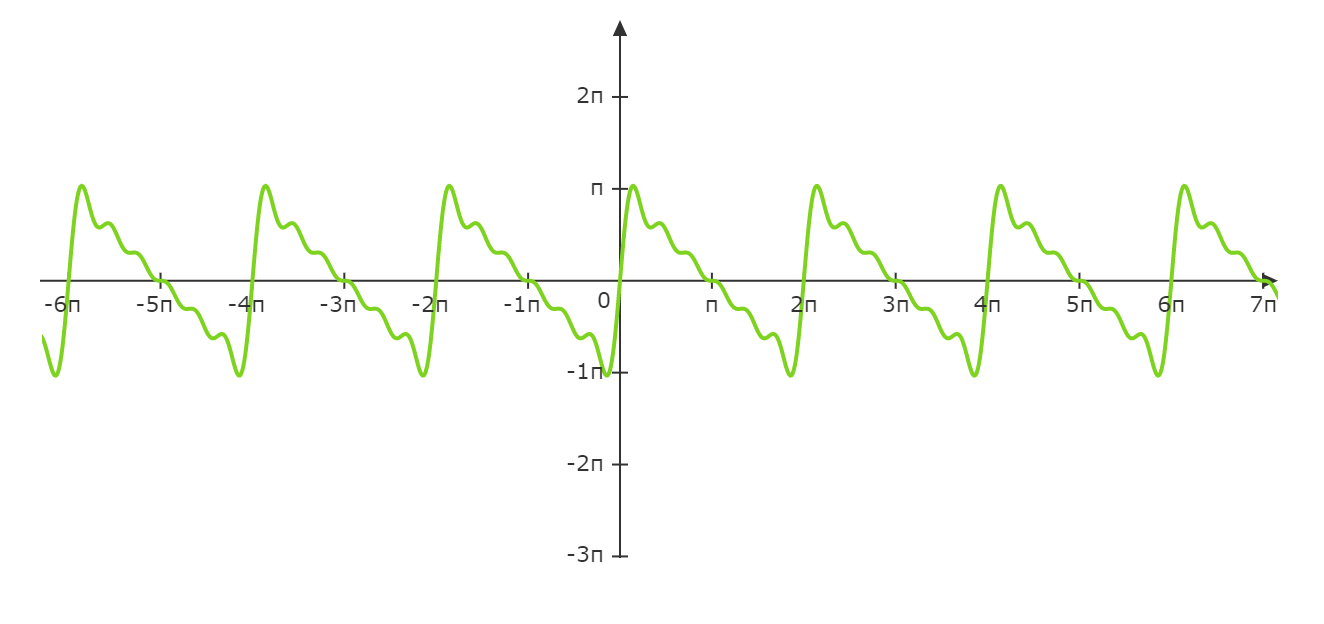
前6项时:
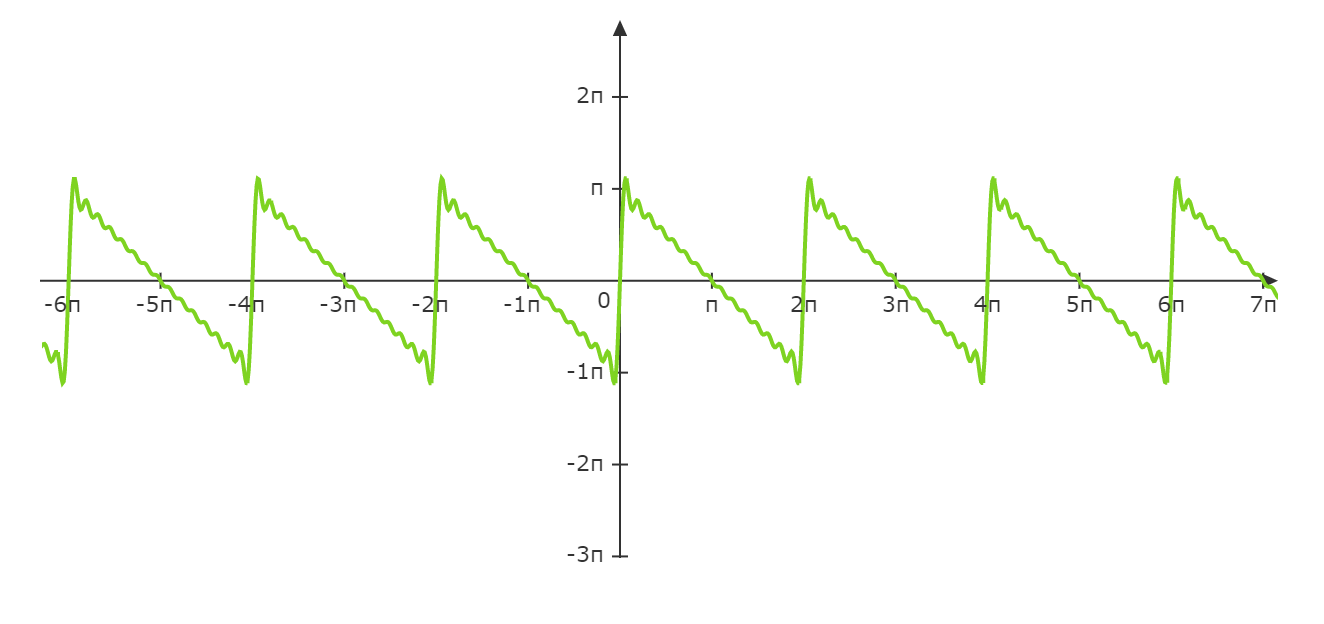
前15项时:
可以断定,当n趋向于无穷时,傅里叶级数无限逼近原函数。
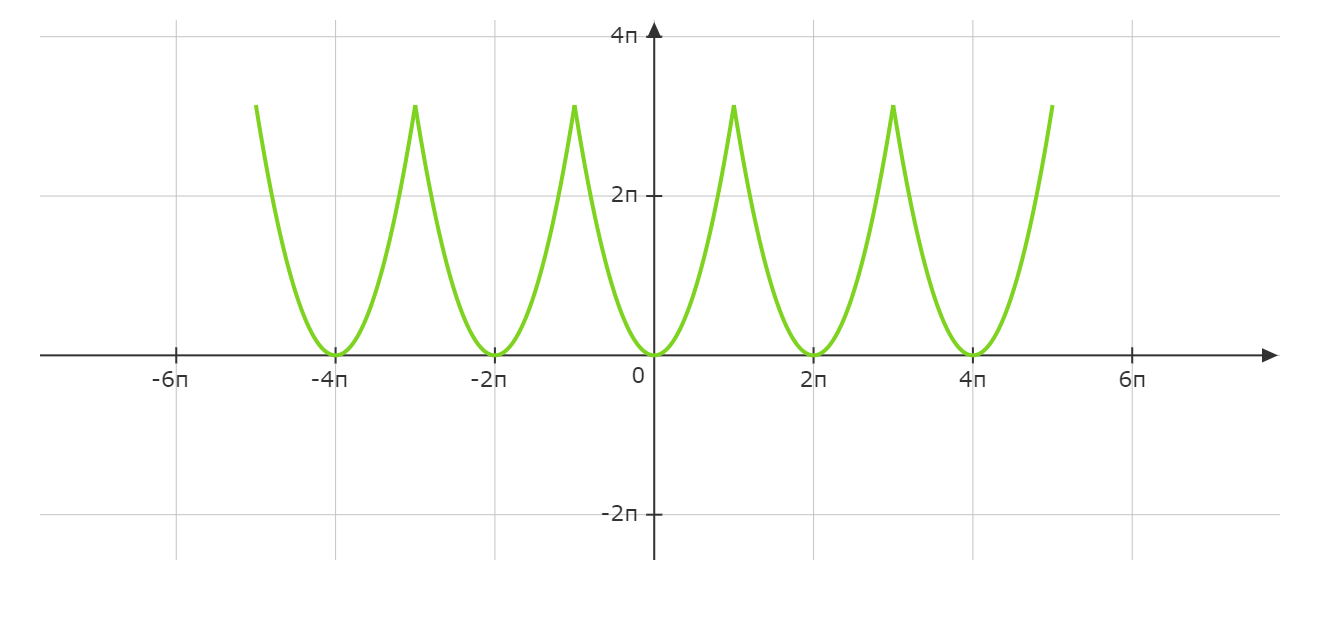
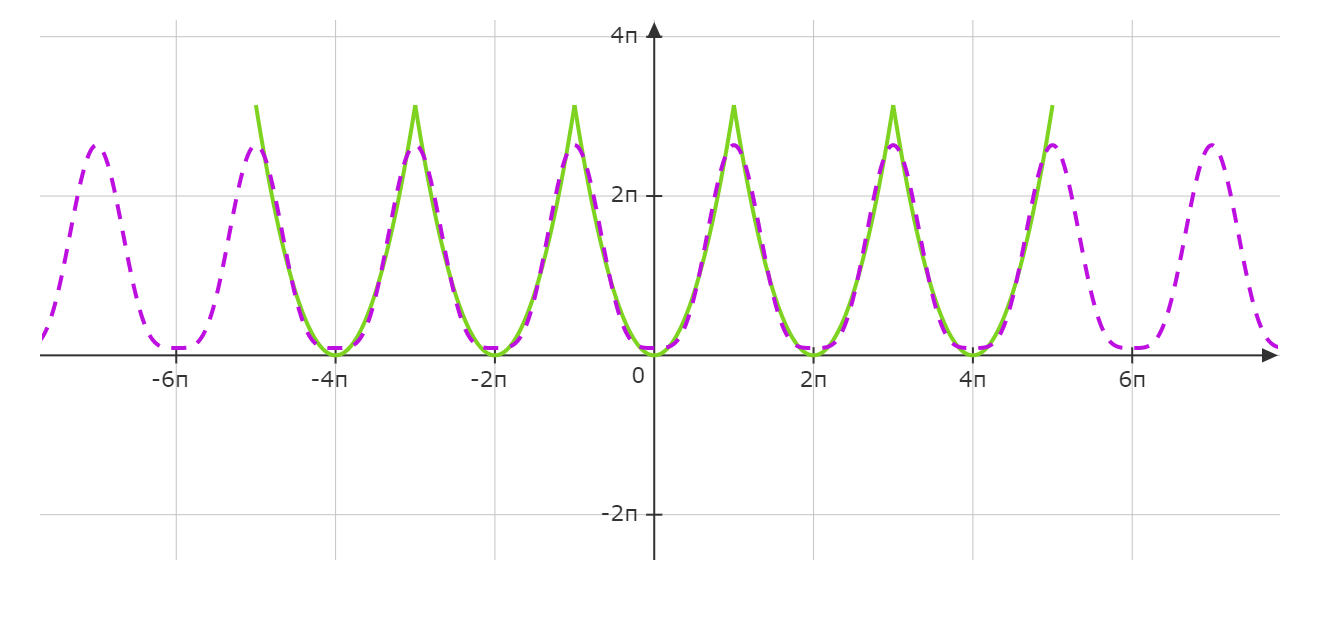
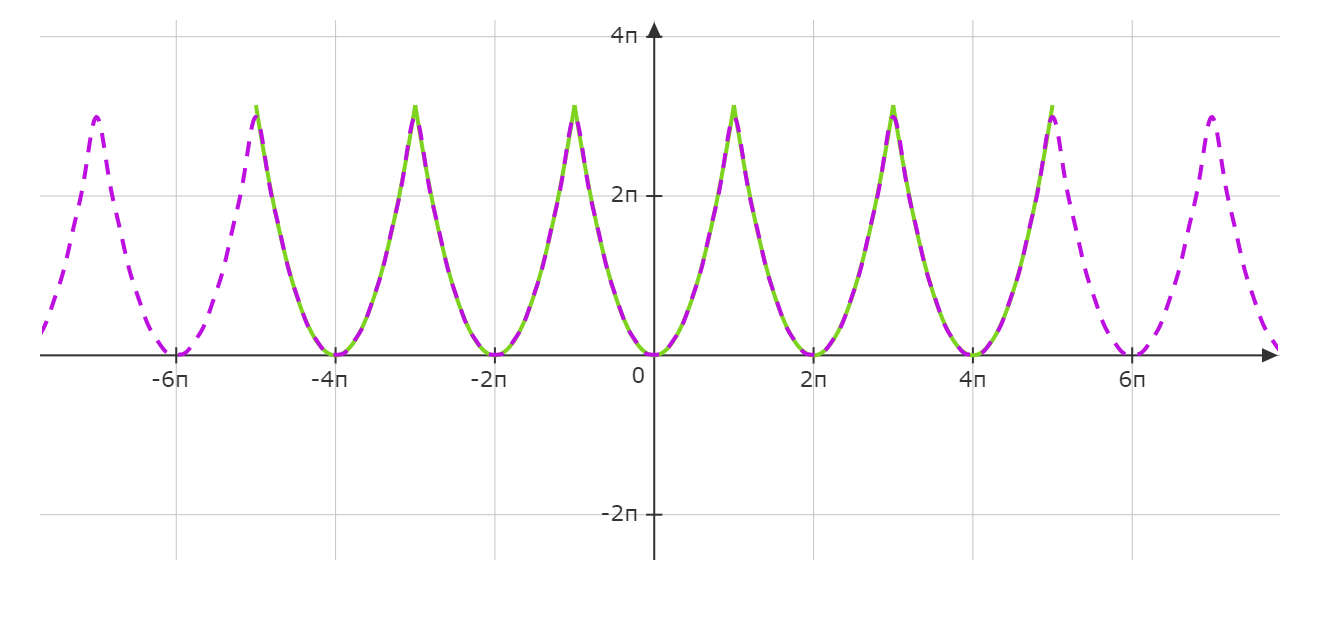
在上面的例子中,我们不管三七二十一就直接计算傅里叶系数\(a_{\nu}\)和\(b_{\nu}\),但其实有简单的方法判断需只要计算其中一个,这跟函数的奇偶性质有关,按照奇偶函数的基本特性:$$两个偶函数的乘积为一个偶函数。(偶×偶=偶)$$$$两个奇函数的乘积为一个偶函数。(奇×奇=偶)$$$$一个偶函数和一个奇函数的乘积为一个奇函数。(偶×奇=奇)$$所以当\(f(x)\)为偶函数时,因为\(\sin\)是奇函数,\(\cos\)是偶函数,根据三角函数的正交特性$$b_{\nu}=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin \nu x dx=0$$当\(f(x)\)奇函数时$$a_{\nu}=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos \nu x dx=0$$在上述公式中,函数$$\ f(x) = \begin{cases} \pi -x, & \quad 当 x > 0\\ 0, & \quad 当x=0,\\ -\pi-x, & \quad 当x<0 \end{cases}$$满足\(f(x)=-f(-x)=-\pi-x\)或 \(f(-x)=-f(x)=-\pi+x\),所以它是奇函数,因此它的系数\(a_{\nu}\)也等于0.对于函数$$f(x)=x^2$$该函数的图像是:同样该函数原本不是周期函数,现在假设它以\(2\pi\)为周期,我们对函数进行了周期延拓,求它的傅里叶展开式。因为它是一个偶函数,所以$$b_{\nu}=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin \nu x dx=0$$又因为它是关于\(y\)轴对称的,所以$$a_{\nu}=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos \nu x dx=\frac{2}{\pi}\int_{0}^{\pi}x^2\cos \nu x dx$$先使用换元积分法,令\(u=\nu x\),那么\(x=\varphi(u)=\frac{u}{\nu}\),所以$$=\frac{2}{\pi}\int_{0}^{\pi}\frac{1}{\nu^2}u^2\cos u \varphi'(u)du=\frac{2}{\pi}\int_{0}^{\pi}\frac{1}{\nu^2}u^2\cos u \frac{1}{\nu}du$$$$=\frac{2}{\pi\nu^3}\int_{0}^{\pi}u^2\cos u du$$再使用分部积分法,令$$f(u)=u^2, \qquad g\,'(u)=\cos u$$$$f\,'(u)=2u, \qquad g(u)=\sin u$$根据分部积分法则$$\int f(u)g\,'(u)=f(u)g(u) - \int f\,'(u)g(u)du$$$$=\frac{2}{\pi\nu^3}\Big(u^2\sin u - \int_{0}^{\pi}2u\sin u du\Big)$$$$=\frac{2}{\pi\nu^3}\Big(u^2\sin u - 2\int_{0}^{\pi}u\sin u du\Big)$$再一次使用分部积分法,令$$f(u)=u, \qquad g\,'(u)=\sin u$$$$f\,(u)=1, \qquad g(u)=-\cos u$$所以$$=\frac{2}{\pi\nu^3}\Big[u^2\sin u - 2(-u\cos u - \int_{0}^{\pi} (-\cos u) du)\Big]$$$$=\frac{2}{\pi\nu^3}\Big[u^2\sin u - 2(-u\cos u + \int_{0}^{\pi} \cos u du)\Big]$$$$=\frac{2}{\pi\nu^3}\Big(u^2\sin u + 2u\cos u - 2\sin u\Big) \Big |_0^\pi$$代入\(u = \nu x\)得$$=\frac{2}{\pi\nu^3}\Big[(\nu x)^2 \sin \nu x + 2 \nu x \cos \nu x - 2\sin \nu x\Big] \Big |_0^\pi$$$$=\frac{2}{\pi\nu^3}\Big(0 + 2 \nu \pi \cos \nu \pi - 0\Big) - 0$$$$=\frac{4\nu \pi \cos \nu \pi}{\pi\nu^3}=\frac{4\cos \nu \pi}{\nu^2}$$因为当\(\nu=1,3,5,\cdots\)奇数时,\(\cos\nu\pi=-1\), \(\nu=2,4,6,\cdots\)偶数时,\(\cos\nu\pi=1\), 所以$$=(-1)^{\nu}\frac{4}{\nu^2} \qquad (\nu > 0)$$计算\(a_0\)$$a_0=\frac{2}{\pi}\int_{0}^{\pi}f(x)\cos 0 x dx=\frac{2}{\pi}\int_{0}^{\pi}f(x)dx=\frac{2}{\pi}\int_{0}^{\pi}x^2dx$$$$=\frac{2x^3}{3\pi}\Big |_0^{\pi}=\frac{2\pi^3}{3\pi} - 0=\frac{2\pi^2}{3}$$最后我们可以求得函数\(f(x)=x^2\)的傅里叶展开式:$$f(x)=\frac{a_0}{2}+\sum_{\nu=1}^{\infty}(a_{\nu}\cos \nu x + b_{\nu}\sin \nu x)$$$$=\frac{\pi^2}{3}+4\sum_{\nu=1}^{\infty}\Big(\frac{(-1)^{\nu}}{\nu^2}\Big)\cos \nu x$$$$x^2=\frac{\pi^2}{3}-4\Big(\frac{\cos x}{1^2}-\frac{\cos 2x}{2^2}+\frac{\cos 3x}{3^2}-\frac{\cos 4x}{4^2}+-\cdots\Big)$$当取前2项时
取前8项时
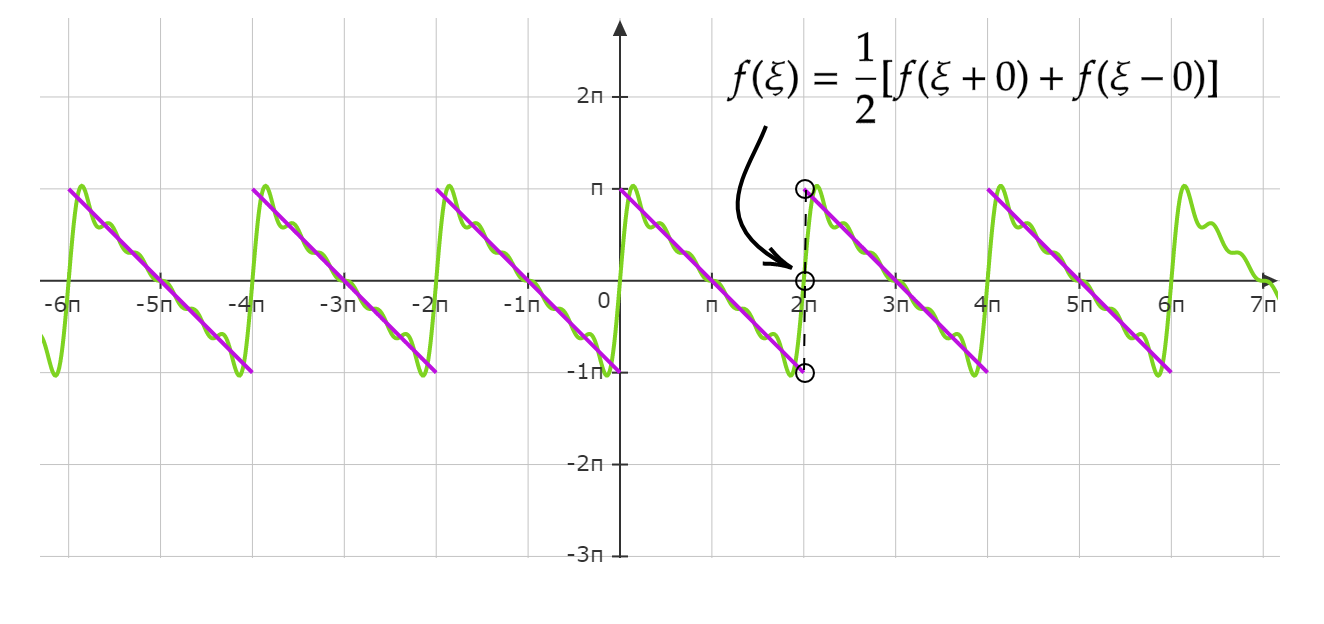
在第一个例子中,我们对函数按照\(2\pi\)周期进行延拓后,出现了跳跃间断点,如果定义跳跃间端点为\(\xi\),那么它的右极限和左极限分别定义为:$$f(\xi + 0)=\lim_{\varepsilon \to 0} f(\xi + \varepsilon^2)$$$$f(\xi - 0)=\lim_{\varepsilon \to 0} f(\xi - \varepsilon^2)$$借助这个约定,我们将原来的函数从闭区间\(a \leq x \leq b\)上周期地开拓到\(x\)的全部值,即使在\(f(a) \neq f(b)\)的情况中也可以。为了定义周期的开拓,采用$$f(\xi)=\frac{1}{2}[f(\xi + 0) + f(\xi - 0)]$$来替代\(f(a)和f(b)\)的值。在例1中,函数在\(n\pi\)处存在间断点,当\(x=\pi\)时,$$f(x)=f(\pi)=\pi - x = \pi - \pi = 0$$当\(x=-\pi\)时,$$f(x)=f(-\pi)=-\pi - x = -\pi + \pi = 0$$所以函数在左极限和右极限的值均为0,因此该函数在间断点趋向于0.以非周期函数采用周期延拓的方式来分段逼近一个函数时,在越靠近间断点时,这些函数变化越快。