曲线的凹凸性与拐点
发布于 2023/07/06 更新于 2023/07/06
作者 趣宽科技 码云上的源文件
码云上的源文件
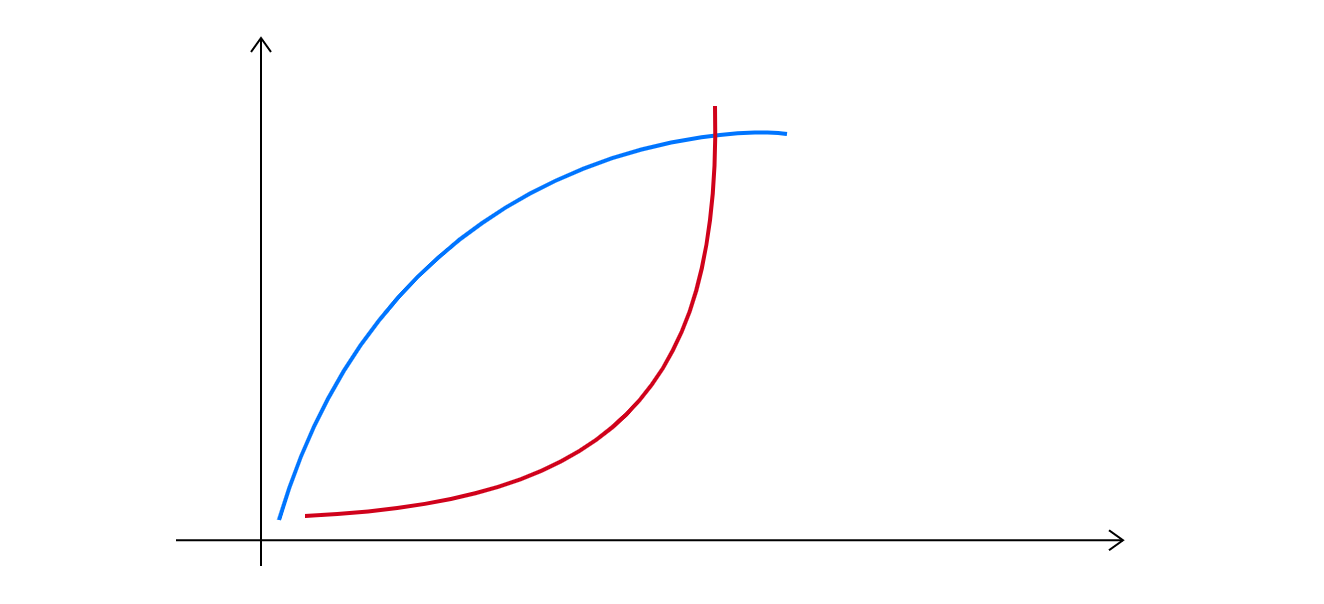
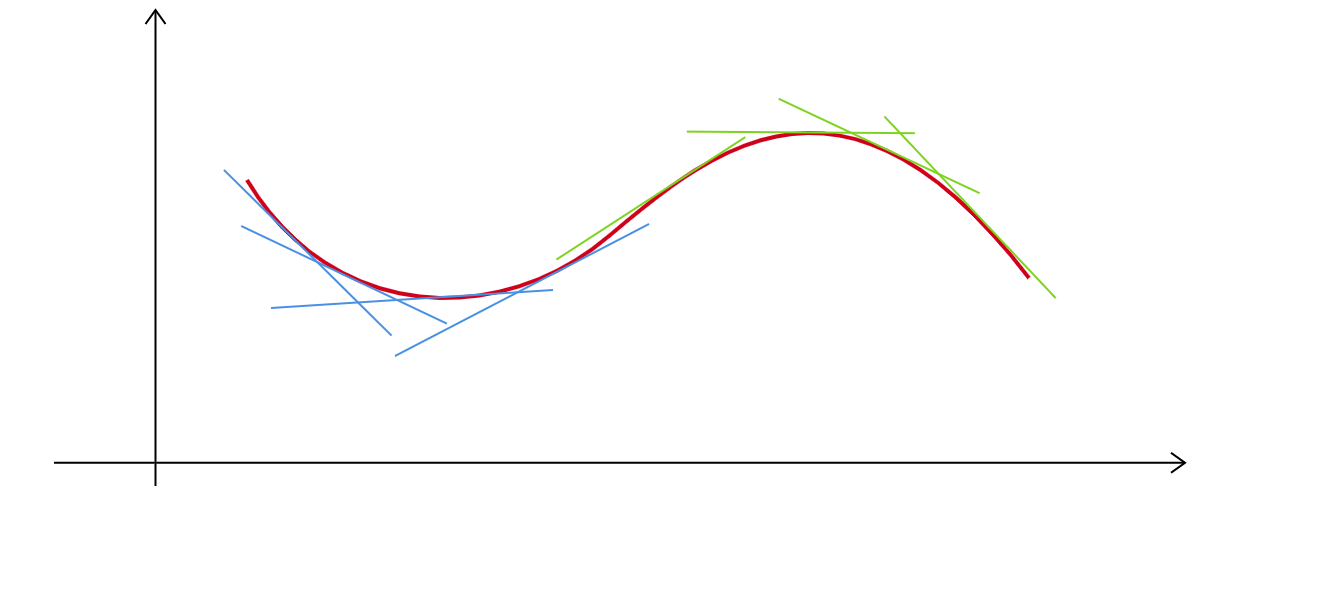
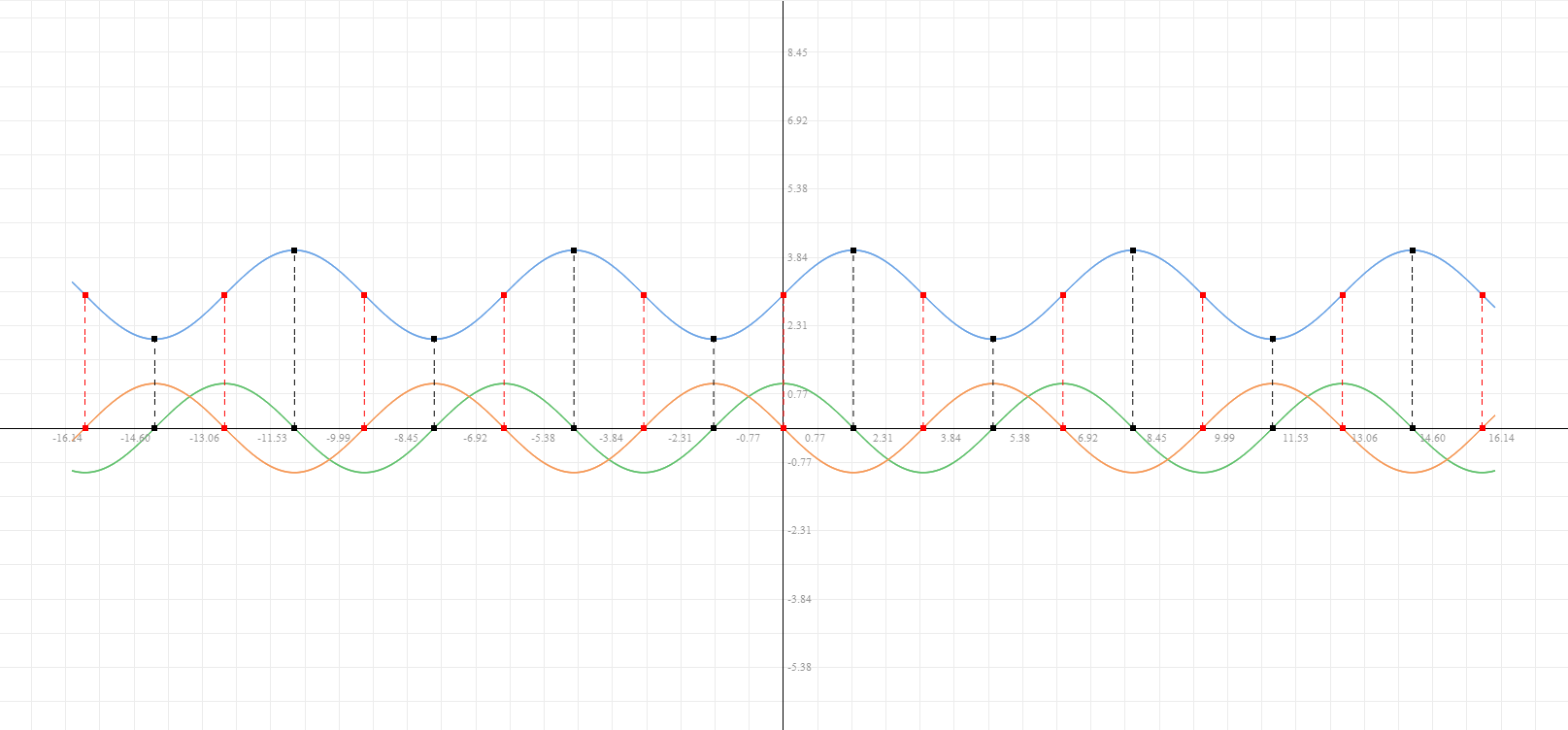
观察两条曲线的上升方式
虽然它们都上升,但是上升的方式不一样:红色曲线上升速度在增加;而蓝色曲线上升速度在减少。两条曲线也有明显不同的弯曲方式,红色曲线是凹升,蓝色曲线是凸升。
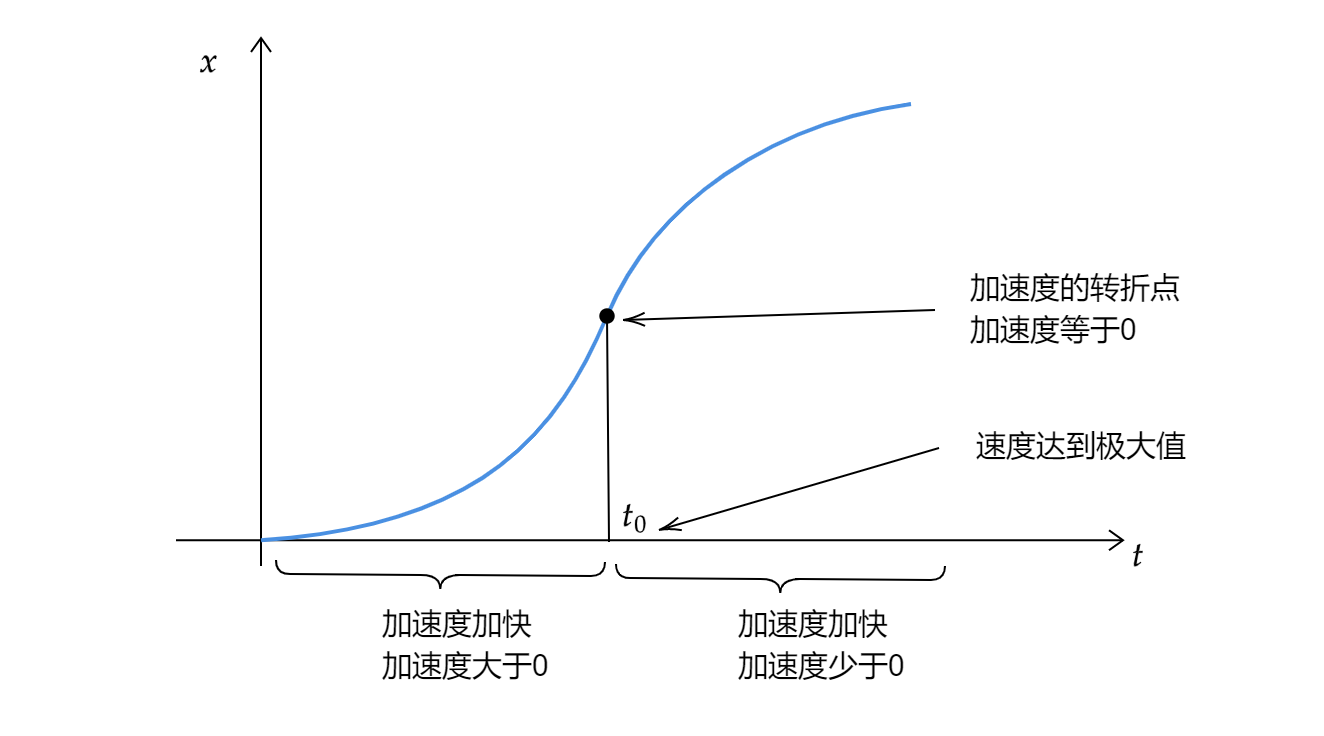
设做直线运动的物体的运动方程是:\(x=x(t)\),\(x\)是\(t\)的函数,它表示位置或距离,如下图所示:
当函数图形处于凹的时候,加速度加快,加速度大于零(相当于函数的二阶导数大于零),而函数图像处于凸的时候,加速度少于零(函数的二阶导数少于零)。在函数在拐点处,速度达到极大值。
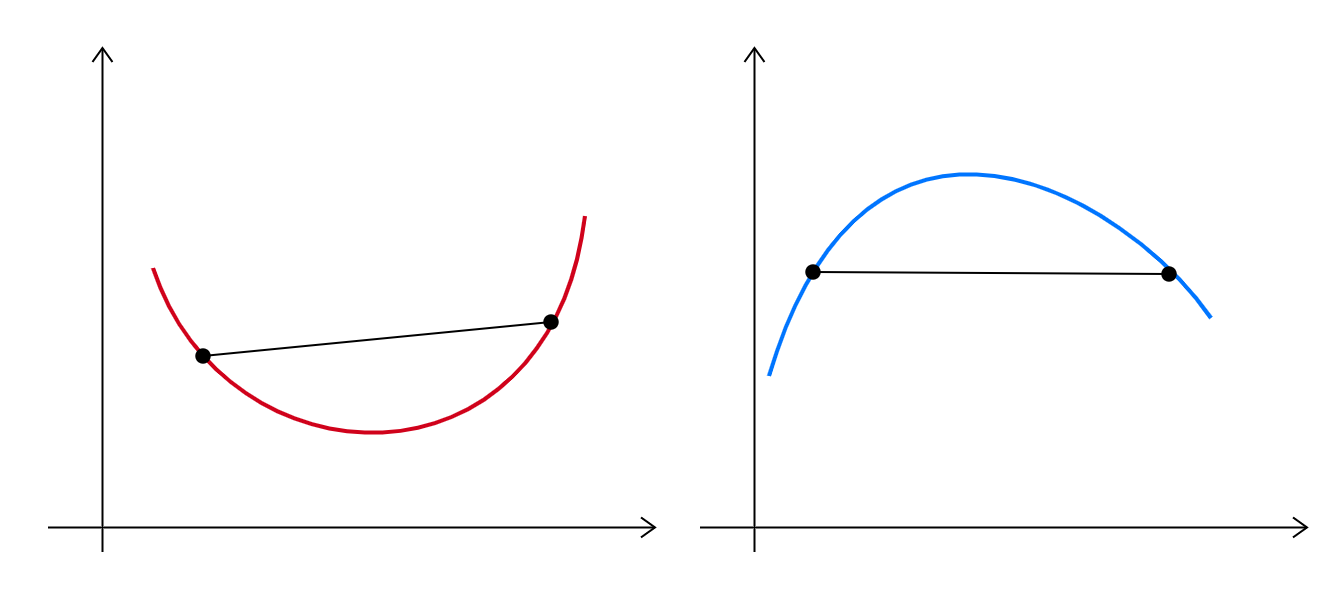
上面说明了曲线凹升和凸升,对应的分别是上凹和上凸
上图分别表示上凹和上凸,在曲线上任意找两点,作一条割线,很明显这条割线在上凹的曲线切割的部分的上方;在上凸的曲线切割部分的下方。
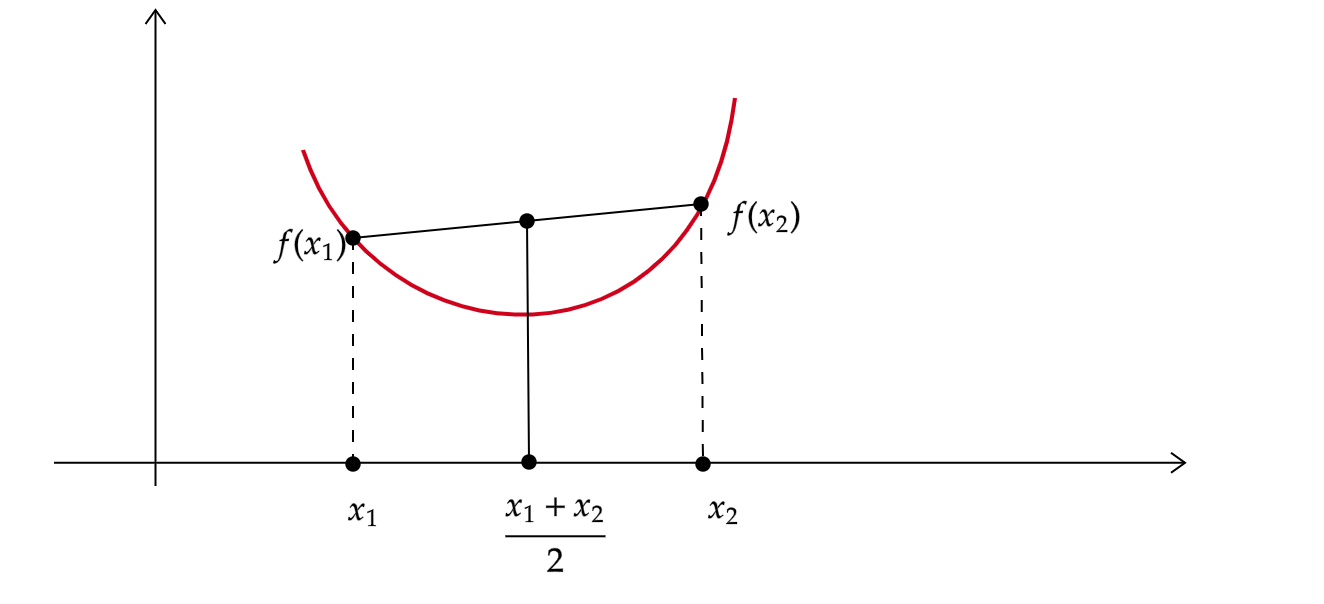
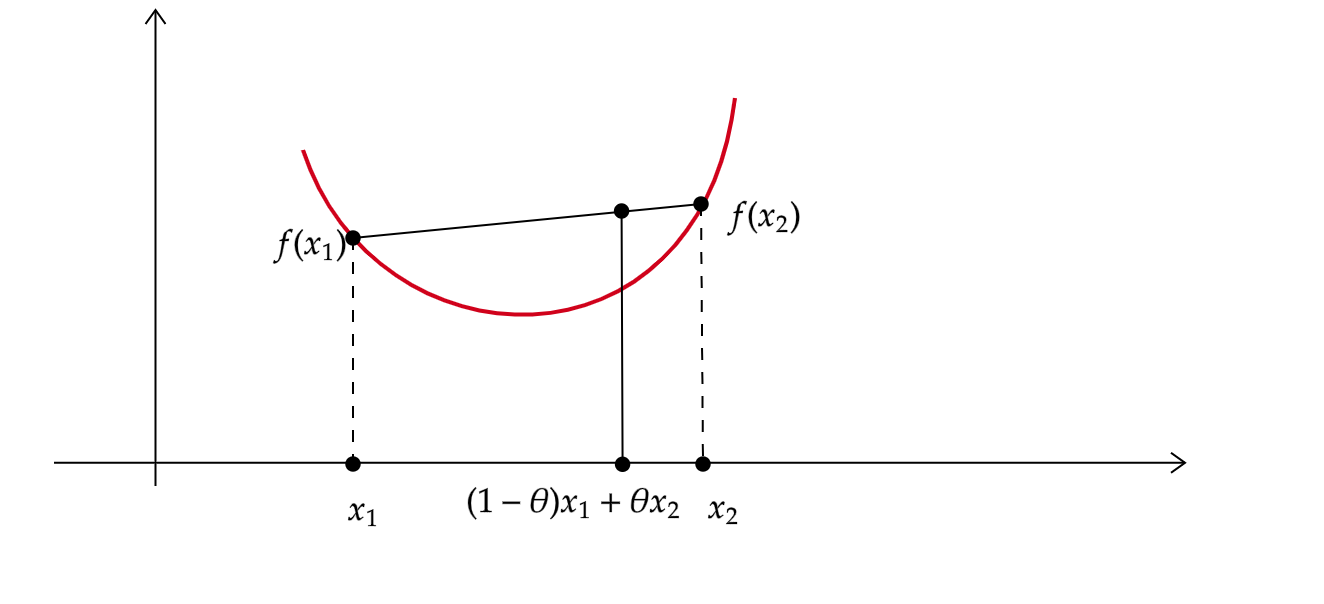
取\(x_1, x_2\)的中点\(\frac{x_1+x_2}{2}\),很显然凹弧的定义
$$
f(\frac{x_1+x_2}{2}) < \frac{f(x_1) + f(x_2)}{2}
$$
因为\(\frac{f(x_1) + f(x_2)}{2}\)是梯形的中位线。它与\(x\) 轴的垂直距离大于该中点到曲线的垂直距离,类似地,上凸曲线有:
$$
f(\frac{x_1+x_2}{2}) > \frac{f(x_1) + f(x_2)}{2}
$$
也可以不取\(x_1,x_2\)的中点,取其间任意一点,因此凹弧的一般定义:
$$
f[(1-\theta)x_1+\theta x_2] < (1-\theta)f(x_1) + \theta f(x_2) \quad (0 < \theta < 1)
$$
曲线的上凹说明它的切线斜率是逐步增加的,上凸说明斜率是逐步减少的。因为切线斜率代表了曲线的导数,因此它的导数是单调增加或单调减少。\( f’(x) \)单调增加。因此它的二阶导数\(f''(x) > 0\),而对于凸弧,它的\(f'(x)\)单调减少,因此\(f''(x) < 0\)。因此可利用一阶导数的单调性判断凹凸性。关于函数的单调性,请看函数的单调性。
设函数\(f(x)\)在\([a, b]\)上连续,在\((a,b)\)内可导,那么,若在\((a,b)\)内\(f'(x)\)单调增加,则曲线\(f(x)\)在\([a,b]\)上是凹的。若在\([a,b]\)内\(f'(x)\)是单调减少的,则曲线\(f(x)\)在\([a,b]\)上是凸的。同时,由此可知:
$$
f''(x) > 0 \implies f'(x) 单增, f''(x) < 0 \implies f'(x) 单减
$$
所以函数的凹凸性判定定理是:若在\((a,b)\)内\(f''(x) > 0\)则函数在\([a,b]\)上是凹的。若\(f''(x) < 0 \)则函数是凸的。
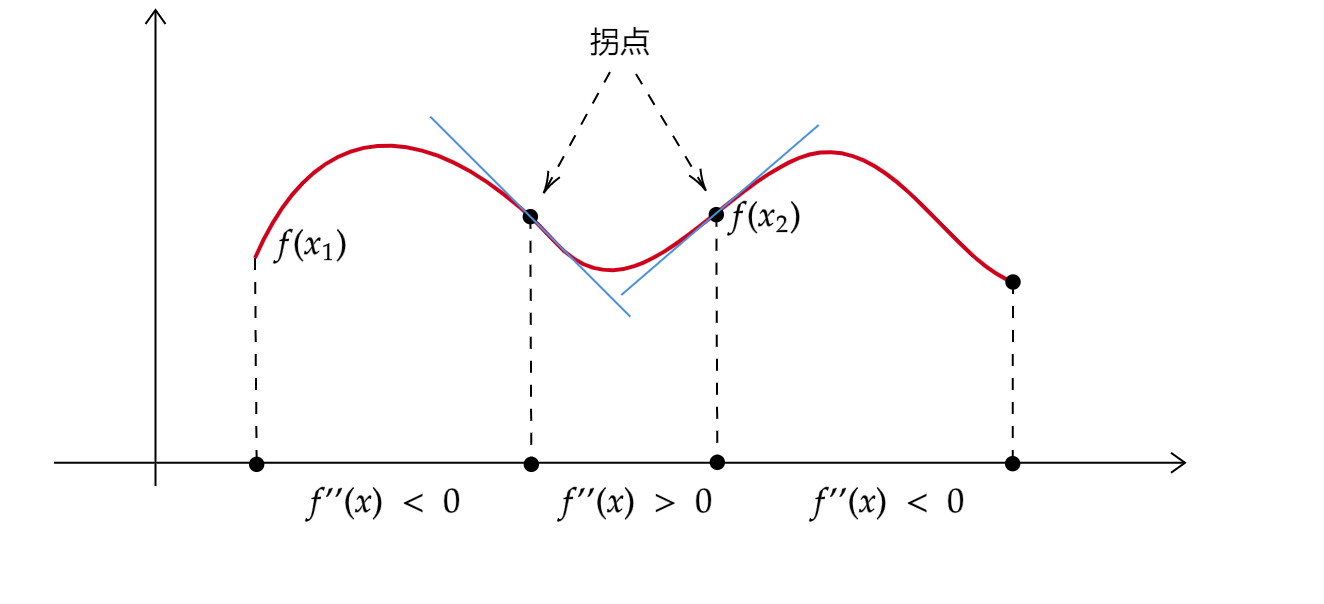
函数出现拐点的地方,可能是二阶导数\(f''(x) = 0\)或\(f''(x)\)不存在。
一阶导数的符号决定函数的单调性,\(f'(x) > 0 \)函数是单调增加的, \(f'(x) < 0\)函数是单调减少的。而\(f''(x) > 0\)函数是凹的,\(f''(x) < 0\)函数是凸的
1. 求出函数\(f(x)\)在区间内二阶导数等于零的点和二阶导数不存在的点\(x_1, x_2, \cdots, x_n\),这些点将函数的定义域分成若干个小区间。
2. 讨论二阶导数在这些小区间的符号以确定函数的凹凸性。
3.考察二阶导数在以上点两侧的符号,以确定该点是否出现拐点。
求下列曲线的凹凸区间和拐点
$$
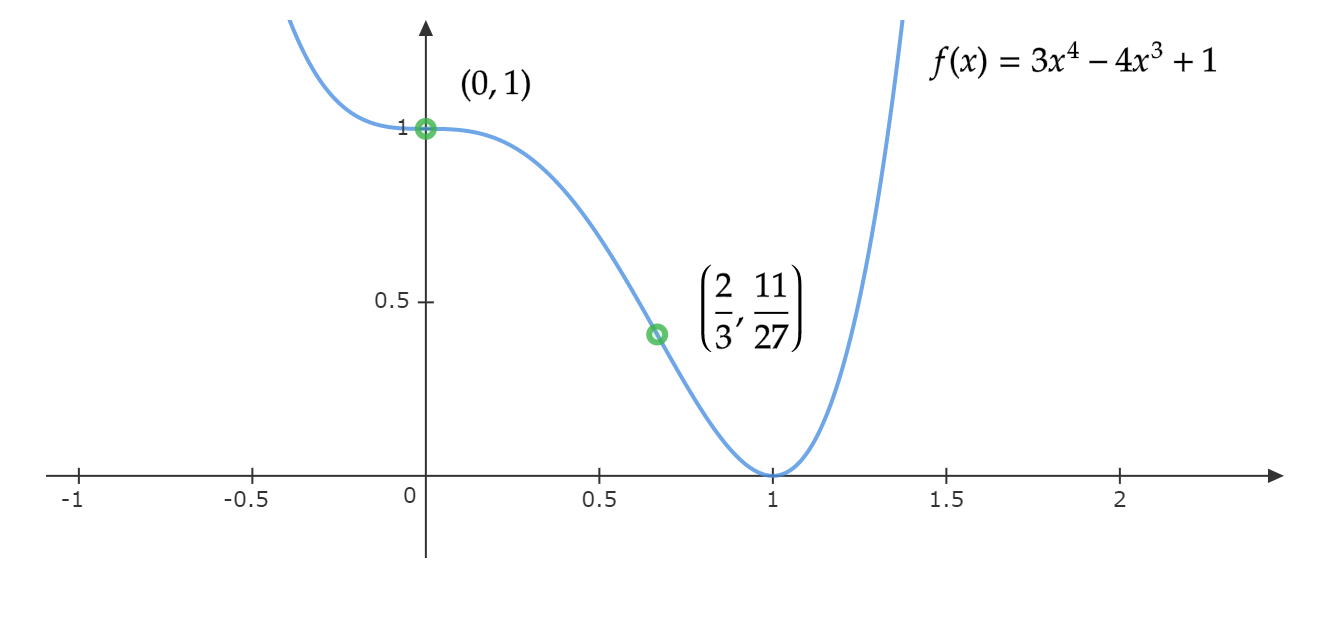
f(x)=3x^4-4x^3+1
$$
$$
f'(x)=12x^3 - 12x^2, \quad f''(x)=36x^2-24x = 36x(x-\frac{2}{3})
$$
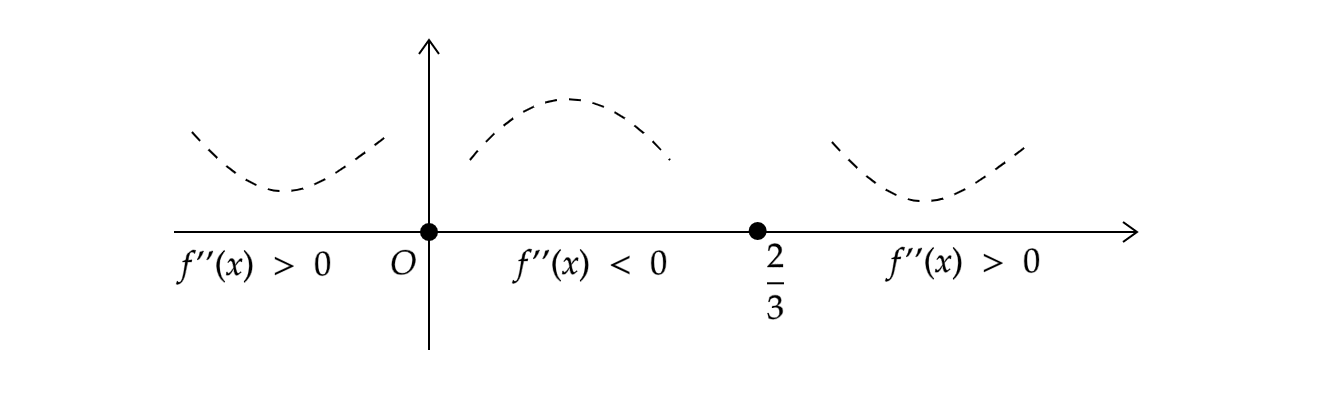
由于该函数的二阶导数处处存在,因此要求拐点只能求使得二阶导数等于0的点。在这里\(x=0, x=\frac{2}{3}\)使得二阶导数等于0,根据函数二阶导数,我们可以知道,在使二阶导数等于零的位置左侧和右侧,我们可以估计得到:
因此函数的凹区间是 \((-\infty, 0)\)和\((\frac{2}{3}, +\infty)\),凸区间是\((0, \frac{2}{3})\),因为0的两侧二阶导数异号且凹凸改变,所以\(0\)是拐点处;同样\(\frac{2}{3}\)处也是拐点。将拐点代入函数得到两个拐点做坐标:
$$
(0,1) ,\quad (\frac{2}{3}, \frac{11}{27})
$$
函数图像如下:
证明使用的定理
$$
f''(x) > 0 \implies f(\frac{x_1 + x_2}{2}) < \frac{f(x_1) + f(x_2)}{2}
$$
和
$$
f''(x) < 0 \implies f(\frac{x_1 + x_2}{2}) > \frac{f(x_1) + f(x_2)}{2}
$$
要证明
$$
e^{\frac{x_1+x_2}{2}} < \frac{e^{x_1}+e^{x_2}}{2} \quad (x_1 \neq x_2)
$$
设\(f(x)=e^x\),因为\(f''(x)=e^x > 0\),曲线是凹的,所以不等式成立。
函数(f(x))的极值点处(f'(x) = 0),拐点处(f''(x)=0)
Qklabs绘制的函数一阶导数、二阶导数以及它们的极值点和拐点
参考: 川大徐小湛《曲线的凹凸性与拐点》