在有两个自变量的函数中，有两种表示方法：其一是可显式地表示，如:$y=f(x)$。即每一个确定的$x$值都有一个唯一确定的$y$值与之对应。另外一种是隐式的表示，如：$x^3+y^3-3xy=0$，它们都是形如$F(x,y)=0$的形式。这些隐函数无法显式地表示出来，也就是说无法转换为$y=f(x)$的形式。因此绘制函数图像无法通过给定的自变量得到对应的因变量的值，也无法通过这种方法在平面直角系上建立函数映射。在前面的文章中我们知道通过Marching Cubes算法实现等值线的绘制。隐函数形如$F(x,y)=c$原理上也可以通过等值线的算法来实现。但是大多数Marching Cubes方法的缺点是它们需要使用非常精细的网格来覆盖区域。当函数图像具有高曲率、高度扭曲或曲线密集时，它不会产生理想的结果，也无法正确处理奇异点和鞍点。

传统方法的缺陷

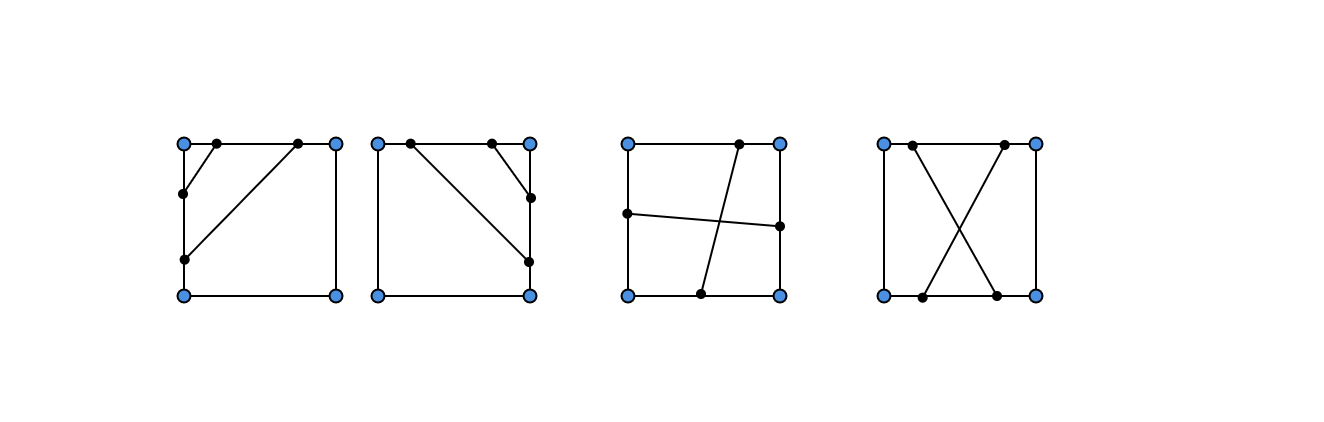
使用Marching Cubes算法会导致一些方格被遗漏。如：存在两条与方格的一条或多条边相交的情况，并且会错过不与方格边相交的小闭合轮廓。绘制任意函数图像时，很难保证检测到所有轮廓线段。因此在实践中，应选择合适的单元格大小以确保：检测到超过一定大小的所有函数线段；每个单元格中最多存在一个线段；以及在单元格内通过直线段进行近似。如果绘图网格不够精细，也可能会出现单元格退化的情况，如下图中的情况：

$/assets/images/article/math/57d7b2dc-3f2d-4da4-848e-4dc563e45f25$

在使用Marching Cubes算法绘制函数$z=x^2+y^2$时，我们选取的网格数量为$16\times 16$时，对于外部轮廓来说看似已经足够了，但对于内部轮廓来说太粗糙了。如果使用更精细的 $32 \times 32$ 网格，则内圈绘制得很好，但外圈迭代次数太多反而没有必要。在整个绘图区域使用相同的均匀网格时，会导致计算资源浪费。

$/assets/images/article/math/d113b3de-1a59-4339-9d8d-cb7110208bc3$

函数$y=x^2+y^2$使用$16\times 16$个网格绘制的等高线

$/assets/images/article/math/f33a3e31-67ad-44ff-89d3-999de5d292bf$

函数$y=x^2+y^2$使用$32\times 32$个网格绘制的等高线

四叉树算法

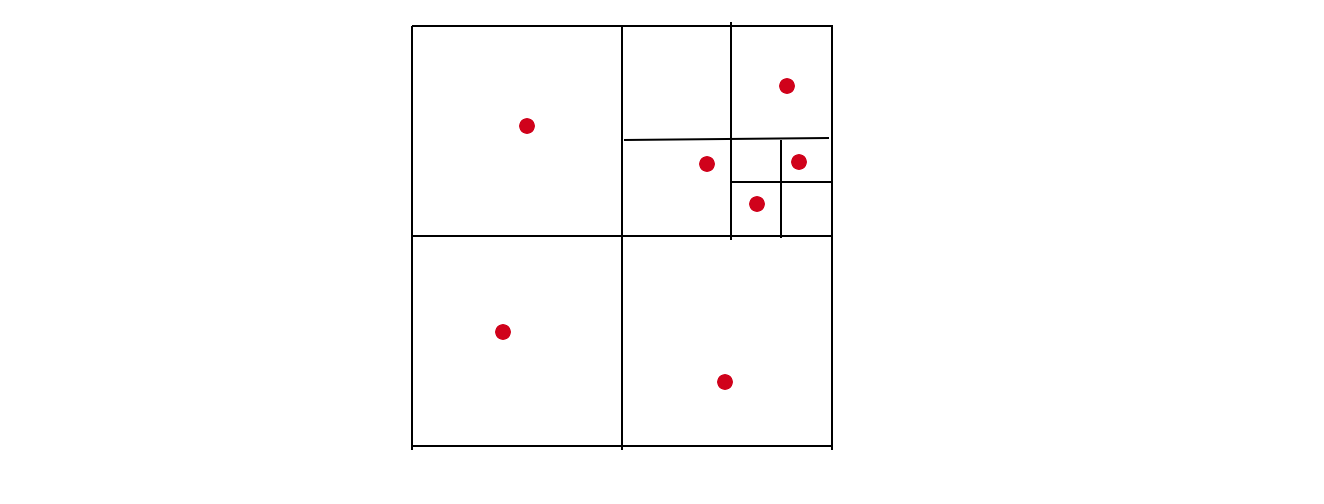
四叉树算法Quadtree Algorithm中的四叉树是一种树状数据结构，在每一个节点上会有四个子区块。四叉树常应用于二维空间资料的分析与分类。在图像压缩、二维地图近邻分析和碰撞监测等方面都有广泛的应用。标准的四叉树算法会把平面均分为四格，该规则对每格能容纳的物体数量有严格限定。在下面的图中，每个子方格只能容纳一个物体，如果物体数量超过该限制后，将在该子方格内继续划分4格子方格空间。直到满足规则要求的为止。在实际应用中，我们往往也会使用非平均分布的四叉树模型，根据不同的需求变量，调整空间权重，形成大小不一的正方形矩形组合。

$/assets/images/article/math/96d1495c-16bc-4f41-8197-d2e008460278$

在初始状态下，我们可以针对函数自变量$x,y$的定义域建立一个$i \times j（行 \times 列)$方格，在每个方格的四个顶点求得函数值。具有两个自变量的隐函数很方便就可以将函数转换为形如$F(x,y)=0$的形式，通过代入$x、y$值求得$z=f(x,y)$。这些方格只作为建立函数曲线的初步轮廓用，在需要进一步细化函数曲线时，则通过四叉树算法建立子方格。

$/assets/images/article/math/d9dafa5c-d633-429d-9253-e4b8e79c3dad$

由于我们要绘制的隐函数都是$F(x,y)=z=0的$的形式，所以如果方格四个顶点的函数值都有相同符号时，根据函数连续性的特征，说明函数线段不经过该方格；如果四个顶点的函数值异号时，函数线段经过方格。我们对方格的四个顶点按照函数值的符号来划分，当$z> 0$时用$\oplus$号标注，当$z<0$时用$\ominus$号标注。

$/assets/images/article/math/b55ec13c-6ed0-4aed-a424-50272ab077f6$

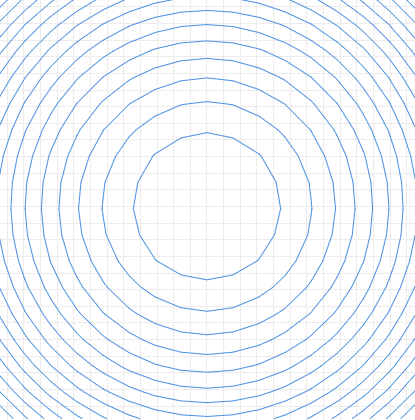
对于上述两种情况，我们认为函数可能至少存在两条线段同时通过该方格，因此需要进一步使用Quadtree算法划分子方格。通过不断迭代，最后绘制出完整的隐函数图像。

因此我们需要设定合适的初始网格$i \times j$的大小。在此基础上，使用Quadtree算法进一步划分子网格。

构造函数图像的点

在下面构造函数图像点的算法中，我们首先排除一些函数不通过方格的情形，当出现可能会多个线段通过方格的情形时，则需要进一步划分子方格。


RectanglePointState QuadTreeRectangle::generateCurvePoints(QList<QVector4D>& listPoints)
{
    if (m_verifyStatus.emtpy) return RectanglePointState::EMPTY;
    uint empty_state = (m_verifyStatus.zero + 1) | m_verifyStatus.pos | m_verifyStatus.neg;
    if ( empty_state >= 4) return RectanglePointState::EMPTY;

    /**
        *  (+)---(-)       (-)---(+)
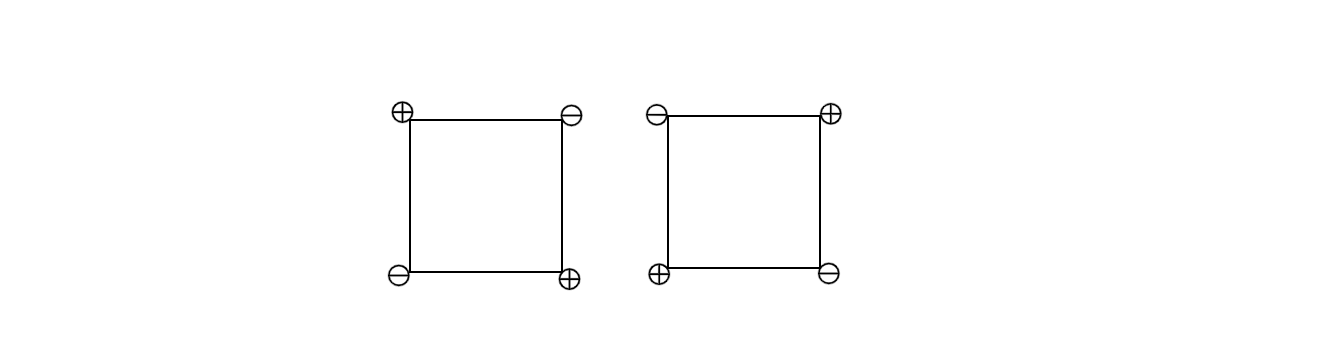
        *  |      |    或   |      |
        *  (-)---(+)       (+)---(-)
        *  如果出现上述情况，函数曲线上的点可能存在于每条边上，因此这种情况需要继续划分子方格。
        */
    if(m_verifyStatus.neg == m_verifyStatus.pos && !oppSign(m_eval.topLeft, m_eval.bottomRight)) return RectanglePointState::T0101;

    switch(m_verifyStatus.zero) {
    case 0:     // 函数曲线上的点都不在矩形的4个顶点上，因此需要通过插值方式计算函数曲线上的点
        {
            if(oppSign(m_eval.topLeft, m_eval.topRight)) {
                float x = interpolate(m_rect.left(), m_rect.right(), m_eval.topLeft, m_eval.topRight);
                listPoints.append(QVector4D(x, m_rect.top(), 0.0f, 1.0f));
            }
            if(oppSign(m_eval.topRight, m_eval.bottomRight)) {
                float y = interpolate(m_rect.top(), m_rect.bottom(), m_eval.topRight, m_eval.bottomRight);
                listPoints.append(QVector4D(m_rect.right(), y, 0.0f, 1.0f));
            }
            if(oppSign(m_eval.bottomRight, m_eval.bottomLeft)) {
                float x = interpolate(m_rect.left(), m_rect.right(), m_eval.bottomLeft, m_eval.bottomRight);
                listPoints.append(QVector4D(x, m_rect.bottom(), 0.0f, 1.0f));
            }
            if(oppSign(m_eval.bottomLeft, m_eval.topLeft)) {
                float y = interpolate(m_rect.top(), m_rect.bottom(), m_eval.topLeft, m_eval.bottomLeft);
                listPoints.append(QVector4D(m_rect.left(), y, 0.0f, 1.0f));
            }
            return RectanglePointState::VALID;
        }

    return RectanglePointState::EMPTY;
}

重要的是，在我们获取函数图形的点时，必须使用线性插值估算当函数值$z=0$时的$x,y$的位置。同时，我们对于使用Quadtree划分子方格的时候必要设定迭代层级。层级太多将耗费太多计算资源并使得绘制效率低下。

线形插值算法

下面的算法用于一般的线性插值算法，假设直线上的两点$P(x_1, y)$, $Q(x_2, y)$，它是一条平行于$x$轴的直线。现在我们要估算中间的一点$R(x,y)$的值$f(x,y)$。线性插值算法如下： $$ f(x,y) = f(x_1, y) + (x - x_1) \frac{f(x_2, y) - f(x_1, y)}{x_2 - x_1} $$ 假设$f(x_1, y) = f_p, f(x_2, y) = f_q$，那么 $$ f(x,y) = f_p + (x - x_1) \frac{f_q - f_p}{x_2 - x_1} $$ 由于我们需要估算的是$f(x,y) = 0$的位置，所以 $$ x=\frac{-f_p}{f_q - f_p}(x_2-x_1) + x_1 $$

隐函数图像示例

$/assets/images/article/math/905b12ff-f1a3-46b4-8678-3c9b09dc3eea$

实现上述法线相关源代请参考Qklabs
更多文章请访问：趣宽科技

目录

四叉树算法和隐函数图像

传统方法的缺陷

四叉树算法

构造函数图像的点

线形插值算法

隐函数图像示例