参数方程和空间曲面
发布于 2023/08/09 更新于 2023/08/09
作者 趣宽科技 码云上的源文件
码云上的源文件
在前面的章节中我们介绍了空间曲面可以通过显式函数或隐式函数来表示。因很多二元函数无法显化,因此显式函能表现的空间曲面类型极其有限,且曲面形状无法调整(比如将抛物面z轴方向的曲面保持平行)。隐式函数几乎可以表示所有二元函数的空间曲面,但必须通过特定的算法,也无法做到调整曲面形状,由于算法的缘故,隐函数曲面在计算过程中难免会增加交叉冗余的曲线,曲面的表面不够光滑。在空间解析几何中,使用参数方程可以很好的表达空间曲面,提高曲面光滑度和通过参数对曲面形状的调整,从而实现显示和隐式函数无法表现的空间曲面效果。
本文分析了常用的参数方程推导过程以及如何通过算法在OpenGL中绘制它们的曲面,帮助用户了解在三维空间中常用曲面的空间解析几何算法和实现过程。
设空间曲线的参数方程为:
$$
\
\begin{cases}
x = \varphi(t) \\
y = \psi(t) && (a \leq t \leq b) \\
z = \omega(t)
\end{cases}
\
$$
设圆心处于原点位置,曲线上的点\(P(\varphi(t), \psi(t), \omega(t))\)绕\(z\)轴旋转,因动点的高度\(z=\omega(t)\)保持不变,所以动点到\(z\)轴的距离是(旋转半径)为:
$$
r(t) = \sqrt{\varphi(t)^2 + \psi(t)^2}
$$
如下图所示,在极坐标系下,圆的方程可表示为:
$$
\
\begin{cases}
x = r(t)\cos\theta \\
y = r(t)\sin \theta
\end{cases}
\
$$
由此可以得到旋转曲面的参数方程:
$$
\
\begin{cases}
x = \sqrt{\varphi(t)^2 + \psi(t)^2} \cos \theta \\
y = \sqrt{\varphi(t)^2 + \psi(t)^2} \sin \theta && (a \leq t \leq b, 0 \leq \theta \leq 2\pi) \\
z = \omega(t)
\end{cases}
\
$$
如下图所示,\(zOx\)面上的半圆
$$
\
\begin{cases}
x = a\sin \varphi \\
y = 0 && (0 \leq \varphi \leq \pi) \\
z = a\cos \varphi
\end{cases}
\
$$
这里的\(a\)表示半径,绕\(z\)轴旋转得球面,求该球面的参数方程。
我们可以求得旋转半径
$$
r(t) = \sqrt{(a\sin \varphi)^2 + 0^2} = a\sin \varphi
$$
根据上述旋转曲面的参数方程,代入\(r(t)\)后得到球面的参数方程:
$$
\
\begin{cases}
x = a \sin \varphi \cos \theta \\
y = a \sin \varphi \sin \theta && ( 0 \leq \varphi \leq \pi, 0 \leq \theta \leq 2\pi) \\
z = a \cos \varphi
\end{cases}
\
$$
上述公式中,\(a\)表示半径,\(\varphi\)是圆的弧度,相当于线条上的点与\(z\)轴的夹角,\(\theta\)是绕\(z\)轴旋转时与\(x\)轴的夹角,我们也可以计算得到:
$$
x^2+y^2+z^2 = a^2\sin^2\varphi\cos^2\theta + a^2\sin^2\varphi \sin^2\theta + a^2\cos^2\varphi
$$
$$
=a^2[\sin^2\varphi\cdot(\cos^2\theta + \sin^2\theta) + \cos^2\varphi]
$$
所以可以得到:
$$
x^2+y^2+z^2=a^2
$$
结果是它与球面方程是一致的。它的图形如下:
我们知道抛物面方程是
$$
z=x^2+y^2
$$
现令\(r=\sqrt{z},z=r^2\),根据旋转曲面的参数方程可得到旋转抛物面的参数方程:
$$
\
\begin{cases}
x = r\cos\theta \\
y = r\sin\theta && ( a \leq r \leq b, 0 \leq \theta \leq 360) \\
z = r^2
\end{cases}
\
$$
该曲面的函数图形如下:
它是由直线:
$$
x=1, y=t, z=2t \quad (-2 \leq t \leq 2)
$$
绕\(z\)轴旋转而成的旋转曲面。因半径\(r=\sqrt{1+t^2}\),故它的曲面参数方程为
$$
\
\begin{cases}
x = \sqrt{1+t^2} \cos \theta \\
y = \sqrt{1+t^2} \sin \theta && (-2 \leq t, 0 \leq \theta \leq 2\pi) \\
z = 2t
\end{cases}
\
$$
该曲面的图像如下:
上面介绍的旋转曲面参数方程使用了旋转半径来建立参数方程,下介绍通过旋转变换来建立旋转曲面参数方程,在通过二维旋转绘制线段箭头一文中,我们介绍了平面上旋转的公式。
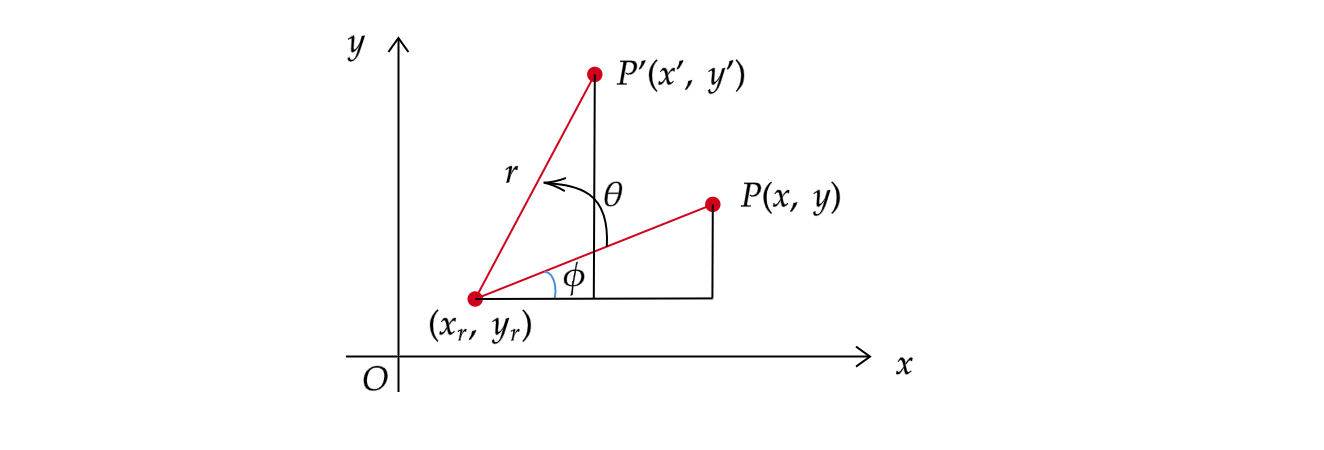

用这个参数方程绘制的曲面有两组母线:一组母线是纬线,另一组母线是曲线在旋转过程中留下的痕迹(动直线)
双叶双曲面是由曲线方程\(x=t, y = t^2, z=t^3 \quad (-1 \leq t \leq 1)\)绕\(z\)轴旋转一周得到的曲面,它的参数方程是:
$$
\
\begin{cases}
x = t\cos\theta - t^2\sin\theta \\
y = t\sin\theta + t^2\cos\theta && (-1 \leq t \leq 1, 0 \leq \theta \leq 2 \pi) \\
z = t^3
\end{cases}
\
$$
它的函数图形如下:
求\(yOz\)面上的圆:\((y-a)^2+z^2=R^2 \quad (0 < R < a) \)绕\(z\)轴旋转一周得到的旋转曲面参数方程。通过该方程我们可以得知,该圆是以\((a, 0)\)为圆心,半径为\(R\)的圆,如下图所示:
通过该方程我们可以求得到\(y=a\pm\sqrt{R^2-z^2},z=\sqrt{R^2-(y-a)^2}\)该圆的参数方程,由于\(\sqrt{R^2-z^2}=a+R\cos (t) = y, \sqrt{R^2-(y-a)^2}=R\sin (t)=z\),通过上面的旋转变换公式可以得到该圆的旋转曲面参数方程:
$$
\
\begin{cases}
x = 0 \cdot \cos \theta - (a + R\cos t) \sin \theta = -(a + R\cos t) \sin \theta \\
y = 0 \cdot \sin \theta + (a + R\cos t) \cos \theta = (a + R\cos t) \cos \theta \\
z = R\sin t \qquad (0 \leq t \leq 2\pi, 0 \leq \theta \leq 2 \pi,0 < R < a)
\end{cases}
\
$$
该参数方程有4个参数,分别是距离圆心的位置\(a\),圆环半径\(R\),圆环上的点和\(y\)轴的夹角\(t\),旋转角度\(\theta\)。该函数图像如下:

$$
(-\infty < S < +\infty, 0 \leq t \leq 2 \pi)
$$
该函数图形如下:
是一种只有一个面(表面)和一条边界的曲面,也是一种重要的拓扑学结构,它的参数方程如下:
$$
\
\begin{cases}
x = (2 + u\cos \frac{v}{2}) \cos v \\
y = (2 + u\cos \frac{v}{2}) \sin v && (-1 \leq u \leq 1, 0 \leq v \leq 2\pi) \\
z = u \sin \frac{v}{2}
\end{cases}
\
$$
它的函数图形如下:
在Qklabs中实现了上述参数方程的空间曲面,用户可以调整参数观察空间曲面的变化情况。
















