关于梯度

在训练机器学习模型时，对权重和偏差进行初始猜测，然后反复调整这些猜测，直到获得损失可能最低的权重和偏差为止。而梯度下降(Gradient descent）是机器学习中最常用的计算代价函数的方法，它是一个一阶最佳化算法，使用梯度算法法可以找到一个函数向下或向上变化最快的方向，从而获取函数的局部极值。在了解梯度前，先介绍一下导数。

导数

$/assets/images/article/math/02ea0c1f-ac13-490a-a5d6-b87a79f96d65$

取曲线上的一点$P$附近的另一点$P_1$，通过这两点$P、P_1$画一条直线(曲线的割线)，现在，如果点$P_1$沿曲线向点$P$移动，则可料到这条割线将达到极限位置，此极限位置与$P_1$从哪一侧趋向于$P$是无关的。这个割线的极限位置便是切线；因为我们所考的曲线是通过函数$y=f(x)$来表示的，所以我们还必须针对$f(x)$用分析的方法来表述这一几何上的极限过程。根据上图得 $$ \lim\limits_{P_1 \to P}\alpha_1 = \alpha $$ 设$x, y$和$x_1, y_1$分别是点$P, P_1$的坐标，这时，我们立即得到 $$ tan\,\alpha_1=\frac{y_1-y}{x_1 - x}=\frac{f(x_1)-f(x)}{x_1-x} $$ 因此上述求极限的过程（不考虑垂直切线$\alpha=\frac{\pi}{2}$的情况)可由下式来表示 $$ \lim\limits_{x_1 \to x}\frac{f(x_1)-f(x)}{x_1-x}=\lim\limits_{x_1 \to x} tan\,\alpha_1=tan\,\alpha $$ 我们将表达式 $$ \frac{f(x_1)-f(x)}{x_1-x}=\frac{y_1-y}{x_1-x}=\frac{\Delta y}{\Delta x} $$ 称为函数$f(x)$的差商。其中符号$\Delta y$和$\Delta x$分别表示函数$f(x)$和自变量$x$之差分。因此，$\alpha$的正切，即曲线的“斜率”等于函数$f$的差商当$x_1 \to x$所趋向的极限。
我们将这个差商的极限称为函数$y=f(x)$在点$x$处的导数，通常使用拉格朗日(Lagrange)表示法$y\,'=f'(x)$来表示导数，也使用莱布尼兹所用的符号$\frac{dy}{dx}, \frac{df(x)}{dx}或(\frac{d}{dx})(fx)$。导数表现形式可以是： $$ f\,'(x) = \lim\limits_{x_1 \to x}\frac{f(x_1) - f(x)}{x_1-x}=\lim\limits_{h \to 0}\frac{f(x + h)-f(x)}{h} $$ $$ \frac{dy}{dx}=\frac{df(x)}{dx}=f\,'(x)=\lim\limits_{x_1 \to x}\frac{f(x_1)-f(x)}{x_1-x}=\lim\limits_{\Delta x \to 0}\frac{\Delta y}{\Delta x} $$ 我们将比值$\frac{\Delta y}{\Delta x}$称为在区间$[x, x+\Delta x]$上$y对于$$x$的”平均变化率“。而极限$f\,'(x) = \frac{dy}{dx}$则表示$y$对于$x$的”瞬时变化率“，或简称”变化率“。

偏导数

一元函数在平面直角坐标系中可表示为线段，因此求导数相当于求某点处切线的斜率。而多元函数在三维空间中可表示为一个曲面，在多元函数中，除了一个自变量之外，我们指定所有其他自变量以确定的值，而只允许那一个自变量，譬如$x$变动，这函数就变成一个一元函数。我们来研究两个自变量$x$和$y$的一个函数$u=f(x,y)$，并指定$y$以一个确定的固定值$y=y_0=c$。得出函数$f(x, y_0)$为单独一个变量$x$的函数，它可以几何地说成是用平面$y=y_0$取切割曲面$u=f(x,y)$。这样形成的平面上的交线可以用方程$u=f(x, y_0)$表示。如果我们对这个方程用普通方法在点$x=x_0$上求导，假设$f$在领域$(x_0, y_0)$的领域有定义，且导数存在，我们就得到$f(x,y)$在点$(x_0, y_0)$处关于$x$的偏导数。 $$ \lim_{h \to 0}\frac{f(x_0+h, y_0) - f(x_0, y_0)}{h} $$ 几何上看，这个偏导数表示$x$轴的一条平行线与曲线$u=f(x, y_0)$的切线之间的夹角的正切。所以它是曲面$u=f(x,y)$在$x$轴方向的斜率。为了表示偏导数，常用几种不同的符号，其中一种是 $$ \lim_{h \to 0}\frac{f(x_0+h, y_0) - f(x_0, y_0)}{h}=f_x(x_0, y_0)=u_x(x_0, y_0) $$ 如果我们希望强调偏导数是一种差商的极限，我们可以把它表示成 $$ \frac{\partial f}{\partial x}或\frac{\partial}{\partial x}f. $$ 这里我们用一个特别的圆形字幕$\partial$代替在一元函数微分法中常用的$d$，这为了表示我们处理的是多元函数，而对其他自变量的求导，使用完全相同的方式，我们用下面的关系式来定义$f(x,y)$在点$f(x_0, y_0)$对$y$的偏导数： $$ \lim_{h \to 0}\frac{f(x_0, y_0 + h) - f(x_0, y_0)}{h}=f_y(x_0, y_0)=D_yf(x_0, y_0) $$ 因此，当我们对其中一个自变量求导时，把其他的变量看作常量。求两个导数 $$ U_x(x,y)=f_x(x,y)=\frac{\partial f(x,y)}{\partial x}. $$ $$ U_y(x,y)=f_y(x,y)=\frac{\partial f(x,y)}{\partial y}. $$ 偏导数本身都是$(x,y)$的函数。举例来说，函数$u=x^2+y^2$具有偏导数$u_x = 2x$(对$x$求导时，把$y^2$看作常数，因而导数为0）和$u_y=2y$。函数$u=x^3y$的偏导数是$u_x=3x^2y$和$u_y=x^3$
类似地，对于任何$n$个自变量的一个函数$f(x_1, x_2, \cdots,x_n)$，我们定义它关于$x_1$的偏导数为 $$ \frac{\partial f(x_1, x_2, \cdots, x_n)}{\partial x_1} = \lim_{h \to 0} \frac{f(x_1+h, x_2, \cdots, x_n) - f(x_1, x_2, \cdots, x_n)}{h} $$ $$ =f_{x_1}(x_1, x_2,\cdots, x_n)=D_{x_1}f(x_1, x_2, \cdots, x_n), $$

偏导数的几何意义

$/assets/images/article/math/66680719-ab19-44e0-8f51-8fd4fbf0362c$

偏导数 $$ \lim_{h \to 0}\frac{f(x_0+h, y_0) - f(x_0, y_0)}{h}=f_x(x_0, y_0)=u_x(x_0, y_0) $$ 是平面$y=y_0$(在曲面环境下，$y=y_0$表示的是y值固定，$x$和$u$为自变量的平面去取切割曲面$u=f(x,y)$,这样形成的平面上的交线$u=f(x, c)或u=f(x, y_0)$，偏导数$f_x$表示$x$轴的一条平行线与曲线$u=f(x,y_0)$的切线之间的夹角的正切，所以它是曲面$u=f(x,y)$在$x$轴方向的斜率。

$/assets/images/article/math/2727c6ac-b68b-4710-b11a-9ee473b69a57$

所以，当曲面$u=f(x,y)$将$y$视为一个常数时，求$x$的偏导数，它的几何意义是指$y$为常数时的平面与曲面切割形成的交线在$x$轴方向的斜率。当将$x$视为一个常数时，求$y$的偏导数，它的几何意义是指$x$为常数时的平面与曲面切割形成的交线在$y$轴方向的斜率。

方向导数

可微函数$f$的一个基本性质是，他们不仅具有关于$x$和$y$的偏导数--或者可以说，沿$x$轴和$y$轴方向的导数---而且还可以沿任何方向的导数，并且这些导数都可以用$f_x$和$f_y$来表示，所谓沿$\alpha$方向的导数是指，当动点沿着一条与$x$轴的正向夹角为$\alpha$的射线逼近$(x,y)$时，函数$f$在$(x,y)$处关于距离的变化率。对于这条射线上的点$(x+h, y+k)$，$h$和$k$可表示成 $$ h=\rho\cos\alpha, k=\rho\sin \alpha $$ (注意，有些使用$k=\rho \cos\beta，因\beta=\frac{\pi}{2}-\alpha，\cos \beta = \sin \alpha$ ) 其中$\rho=\sqrt{h^2+k^2}$是$(x+h, y+k)到(x,y)$的距离,沿着这条射线，$f$成了$\rho$的函数 $$ f(x+\rho \cos\alpha, y+\rho \sin \alpha) $$

$/assets/images/article/math/fb1e7f77-8c55-4db2-a39e-41cb7a86eea7$

$f$在点$(x,y)$处沿着$\alpha$方向的导数定义为$f(x+\rho \cos\alpha, y+\rho \sin \alpha)$在$\rho=0$处关于$\rho$的导数，并且用$D_{(\alpha)}f(x,y)$表示，因此 $$ D_{(\alpha)}f(x,y)=\Big(\frac{d}{d\rho}f(x+\rho \cos \alpha, y+\rho \sin \alpha)\Big)_{\rho=0} $$ $$ =\lim_{\rho \to 0}\frac{f(x+\rho \cos \alpha, y+\rho \sin \alpha)-f(x,y)}{\rho} $$ 如果这个极限存在的话，特别地，当$\alpha=0$和$\alpha=\frac{\pi}{2}$时， $$ D_{(0)}f(x,y)=\lim_{\rho \to 0}\frac{f(x+\rho\cdot 1, y+\rho \cdot 0) - f(x,y)}{\rho}=\frac{f(x+\rho, y) - f(x,y)}{\rho}=f_x(x,y) $$ $$ D_{(\frac{\pi}{2})}f(x,y)=\lim_{\rho \to 0}\frac{f(x, y+\rho) - f(x,y)}{\rho}=f_y(x,y) $$ 如果$f(x,y)$是可微的，则我们有(类似一元函数导数近似微分的定义）$\Delta y = f'(x)\Delta x + \varepsilon \Delta x$数的定义）： $$ f(x+h, y+k) - f(x,y)=hf_x + kf_y + \varepsilon \rho $$ $$ =\rho(f_x\cos \alpha + f_y \sin \alpha + \varepsilon) $$ 令$\rho \to 0$，于是，由于$\varepsilon \to 0$，我们得到$f$沿$\alpha$方向的导数的表达式 $$ D_{(\alpha)}f(x,y)=f_x\cos \alpha + f_y \sin \alpha $$ 这样，方向导数$D_{(\alpha)}$便是$x$轴方向和$y$轴方向的导数$f_x$和$f_y$的线性组合，系数为$\cos \alpha$和$\sin \alpha$，特别地，当导数$f_x, f_y$在所考虑的点存在而且连续时，上述结果成立。
如果函数$z=f(x,y)$在点$P(x,y)$处可微分，则该函数在该点沿任意一方向的$l$的方向导数都存在，并且 $$ \frac{\partial f}{\partial l } = \frac{\partial f}{\partial x}\cos \alpha + \frac{\partial f}{\partial y}\sin \alpha \quad l=(\cos \alpha, \sin \alpha) $$ 方向导数是曲面$u=f(x,y)$在点$(x,y)$处沿方向向量$(\cos\alpha, \sin \alpha)$的倾斜程度（坡度）上述的公式可记作 $$ \frac{\partial f}{\partial l } = \frac{\partial f}{\partial x}\cos \alpha + \frac{\partial f}{\partial y}\cos \beta $$ $$ \frac{\partial f}{\partial l } = \{ \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \} \cdot \{ \cos \alpha, \cos \beta \} $$ $$ =\text{grad}f \cdot \vec{l^{\circ}} $$ $\text{grad}f$是梯度，如果$\vec{l}$不是单位向量，就把它单位化(向量中各个元素比上自己的模) $$ =\text{grad}f \cdot \frac{\vec{l}}{|\vec{l}|} $$ 三元函数$u=f(x,y,z)$在点$(x,y,z)$沿方向$\vec{l}=\{\cos \alpha, \cos \beta, \cos \gamma\}$的方向导数： $$ \frac{\partial f}{\partial l} = \frac{\partial f}{\partial x}\cos\alpha + \frac{\partial f}{\partial y}\cos\beta + \frac{\partial f}{\partial z}\cos\gamma $$

梯度(Gradient vectors)

梯度是讨论函数变化最快的方向

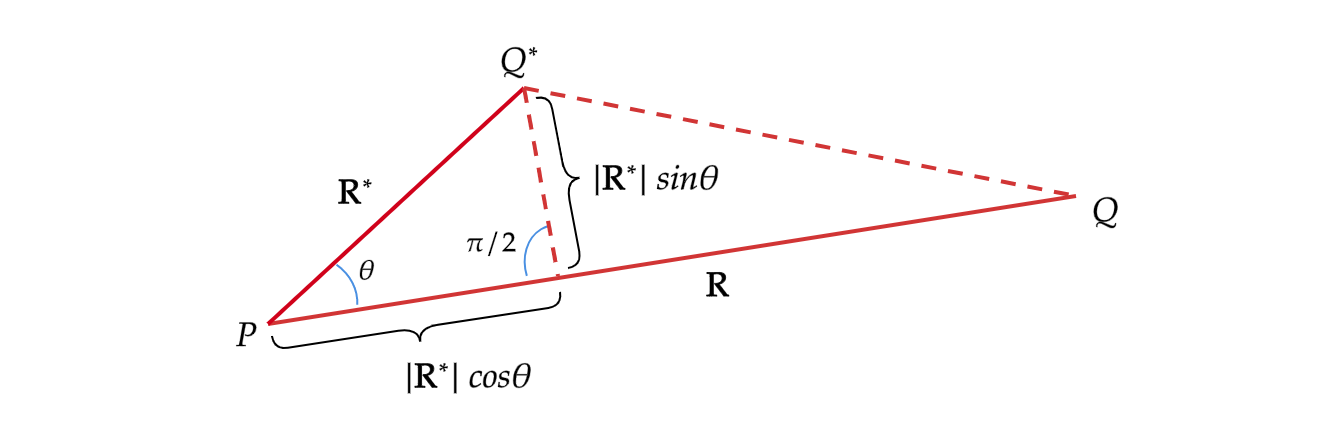
$$ \frac{\partial f}{\partial l} = \Big\{\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\Big\} \cdot \Big\{\cos \alpha, \cos \beta\Big\} $$ $$ =\text{grad}f \cdot \vec{l^{\circ}}=\text{grad}f \cdot \frac{\vec{l}}{|\vec{l}|} $$ 表示函数$f$沿方向向量$l$的方向导数，在几何上，方向导数是曲面$u=f(x,y)$在点$(x,y)$处沿方向向量$l=(\cos\alpha, \sin \alpha)$的倾斜程度（也叫坡度）。令$\textbf{R}$和$\textbf{R}^*$有同一个起点，$\textbf{R}=\overrightarrow{PQ}, \textbf{R}^*=\overrightarrow{PQ^*}$，$\textbf{R}\cdot\textbf{R}^*$可解释为：线段$PQ^*$在线段$PQ$上的射影$r^*cos\,\theta$和该线段长的乘积；外积$\textbf{R}\times \textbf{R}^*$只不过是有向三角形$PQQ^*$的面积的两倍（$\textbf{R}\times \textbf{R}^*=rr^*sin\,\theta$）。如下图所示

$/assets/images/article/math/991d1df1-811b-4d6f-bc30-f238d4b27349$

所以，方向导数

$$ =\text{grad}f \cdot \vec{l^{\circ}}=|\text{grad}f|\cdot|\vec{l^{\circ}}|\cdot \cos \theta $$ 由于单位向量的模$|\vec{l^{\circ}}|$恒等于$1$，所以 $$ =\text{grad}f \cdot \vec{l^{\circ}}=|\text{grad}f|\cdot \cos \theta $$ 当$\theta=0$时，即$\vec{l}$与方向向量$\Big\{\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\Big\}$方向相同时，方向导数取到最大值。 $$ \frac{\partial f}{\partial l} = |\text{grad}f|\cdot \cos 0 = |\text{grad}f| $$ 因此向量$\Big\{\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\Big\}$是使函数在一点的方向导数达到最大值的方向。它也是函数在一点的增加最快的方向。我们称该向量是二元函数$z=f(x,y)$在点$(x,y)$处的梯度向量，简称梯度(Gradient )，记作 $$ \text{grad}f = \Big\{\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\Big\}=\frac{\partial f}{\partial x}i+\frac{\partial f}{\partial y}j = \bigtriangledown f $$ 梯度是一个向量，它是函数$z=f (x,y)$在点$(x,y)$处取得最大方向导数的方向。梯度向量在任何点都垂直于函数的等值线。

梯度上升或下降

梯度下降方法基于以下的观察：如果实值函数$F(x)$在点$a$处可微且有定义，那么函数$F(x)$在$a$点沿着梯度相反的方向$-\bigtriangledown F(a)$下降最多。它可以表示为： $$ X_{n+1}=X_n - \gamma_n \bigtriangledown F(x_n), n \geq 0 $$ 对于二元函数，梯度下降可以表示为： $$ (x_{n+1}, y_{n+1})=(x_n, y_n) - \gamma \times \bigtriangledown f(x_n, y_n) $$ 相应的，梯度上升可表示为： $$ (x_{n+1}, y_{n+1})=(x_n, y_n) + \gamma \times \bigtriangledown f(x_n, y_n) $$ 对于梯度上升或下降，选择合适的迭代步长和迭代次数也很重要。

梯度下降的缺点

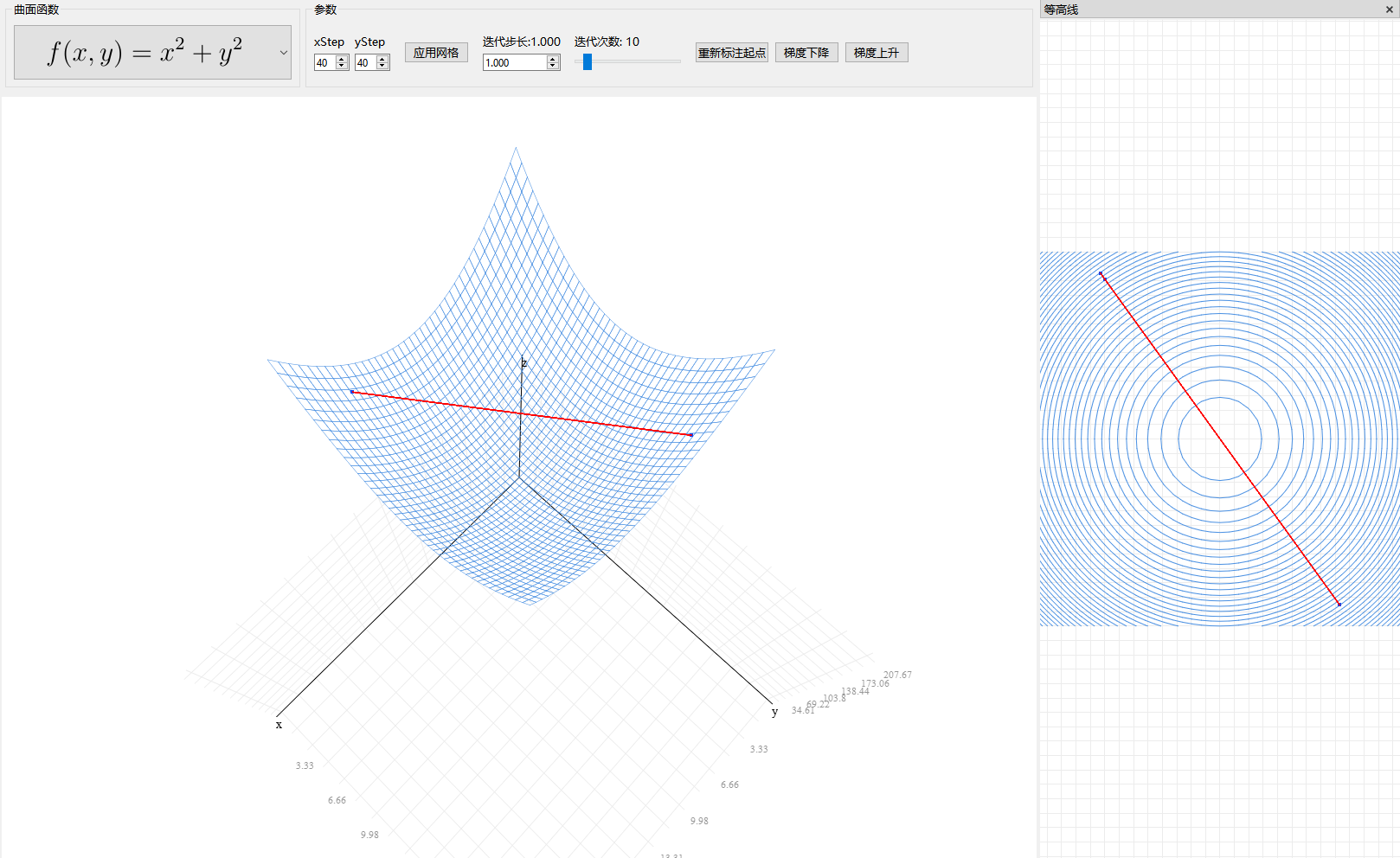
当迭代步长选择过大时，梯度下降在不同的点之间来回震荡。如下图

$/assets/images/article/math/65c40998-06f6-4d73-b9fc-af06af6fa54e$

梯度上升/下降演示

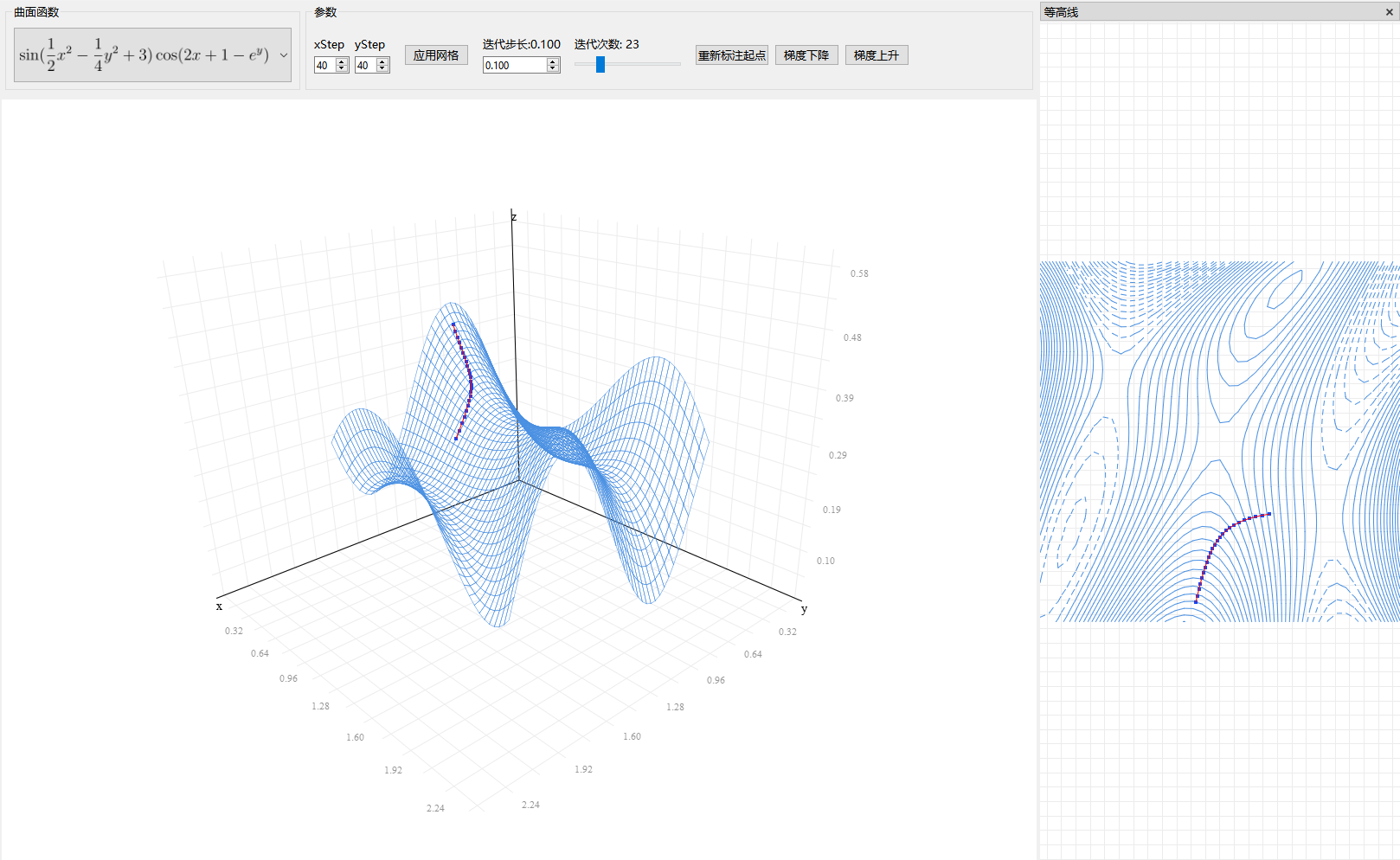
Qklabs通过对一些函数求偏导数和梯度向量，使用OpenGL展示了梯度上升或下降的过程，它可以设置迭代次数和迭代步长，通过标注梯度起始点，形象的展示了梯度上升/下降的过程。

$/assets/images/article/math/7dc2a689-f261-433f-b249-a3a56b6e1a16$

$/assets/images/article/math/f2da0fc5-bfab-43a9-a95d-ce2167a1f5d8$

$/assets/images/article/math/88bdc858-ca1b-4d02-a2ee-2aa547595b84$

示例代码中部分函数的偏导数计算

函数1

$$ f(x,y) = \frac{x}{x^2+y^2+2} $$ 使用商的导数的法则： $$ \varphi(x)=\frac{f(x)}{g(x)} $$ $$ \varphi'(x)=\frac{g(x)f'(x)-g\,'(x)f(x)}{[g(x)]^2} $$ 令$u=f(x)=x，v=g(x)=x^2+y^2+2$得： $$ \frac{\partial f}{\partial x}=\frac{v\cdot \frac{\partial u}{\partial x} - u\cdot \frac{\partial v}{\partial x}}{(x^2+y^2+2)^2} $$ $$ =\frac{(x^2+y^2+2) - x\cdot 2x}{(x^2+y^2+2)^2}=\frac{-x^2+y^2+2}{(x^2+y^2+2)^2} $$ $$ \frac{\partial f}{\partial y}=\frac{v\cdot \frac{\partial u}{\partial y} - u\cdot \frac{\partial v}{\partial y}}{(x^2+y^2+2)^2} $$ $$ =\frac{0 - x\cdot 2y}{(x^2+y^2+2)^2}=\frac{-2xy}{(x^2+y^2+2)^2} $$

函数2

$$ f(x,y)=e^{-x^2}e^y $$ 求偏导导数，利用导数乘积法则： $$ \varphi (x)= f(x)g(x) \implies \varphi'(x)=f(x)g\,'(x) + g(x)f'(x) $$ 令$f(x)=e^{-x^2}, g(x)=e^y$，那么 $$ \frac{\partial \varphi}{\partial x} = e^{-x^2}\cdot \frac{\partial g}{\partial x} + e^y\cdot \frac{\partial f}{\partial x} $$ $$ =e^{-x^2}\cdot 0 + e^y \cdot \frac{\partial}{\partial x}(e^{-x^2}) $$ 令$u=-x^2$，利用链式法则，可得 $$ \frac{\partial}{\partial x}(e^{-x^2}) = e^u \cdot \frac{du}{dx} = -2xe^{-x^2} $$ 故 $$ \frac{\partial f}{\partial x} = e^y \cdot -2xe^{-x^2} = -2xe^{y-x^2} $$ $$ \frac{\partial f}{\partial y} = e^{-x^2}\cdot \frac{\partial g}{\partial y} + e^y\cdot \frac{\partial f}{\partial y} $$ $$ =e^{-x^2}\cdot e^y + e^y\cdot 0 = e^{y-x^2} $$

函数3

$$ f(x,y)=\sin(\frac{1}{2}x^2-\frac{1}{4}y^2+3)\cos(2x+1-e^y) $$ 利用导数乘法法则：令$u=\frac{1}{2}x^2-\frac{1}{4}y^2+3, v = 2x+1-e^y$，得： $$ f(x,y)=\sin u \cos v $$ 令$\varphi(x)=\sin u, g(x)=\cos v$，那么 $$ \frac{\partial f}{\partial x} = \sin u \cdot \frac{\partial g}{\partial x} + \cos v \cdot \frac{\partial \varphi}{\partial x} $$ $$ =\sin u \cdot (-\sin v) \cdot 2 + \cos v \cdot \cos u \cdot x $$ $$ =-2 \sin(\frac{1}{2}x^2-\frac{1}{4}y^2+3) \sin (2x+1-e^y) + x\cos(\frac{1}{2}x^2-\frac{1}{4}y^2+3)\cos(2x+1-e^y) $$ $$ \frac{\partial f}{\partial y} = \sin u \cdot \frac{\partial g}{\partial y} + \cos v \cdot \frac{\partial \varphi}{\partial y} $$ $$ =\sin u \cdot (-\sin v) \cdot (-e^y) + \cos v \cdot \cos u \cdot (-\frac{1}{2}y) $$ $$ =e^y \sin(\frac{1}{2}x^2-\frac{1}{4}y^2+3) \sin (2x+1-e^y) - \frac{1}{2} y\cos(\frac{1}{2}x^2-\frac{1}{4}y^2+3)\cos(2x+1-e^y) $$

关于上述算法的源代代码和演示程序，请访问Qklabs

目录

方向导数和梯度