傅里叶的复数形式
发布于 2023/03/27 更新于 2023/03/27
作者 趣宽科技 码云上的源文件
码云上的源文件
在笛卡尔坐标系中分析傅里叶级数已不能满足需求,通过欧拉公式提供复点至极坐标的变换,使用复平面来分析三角级数必须引入复数,本文主要说明使用欧拉公式来表示傅里叶的复数形式,欧拉公式在数学、物理和工程领域应用广泛。
我们先回顾一下阶数为\(n\)的傅里叶级数公式是$$f(x)=\frac{a_0}{2}+\sum_{\nu=1}^{n}(a_{\nu} \cos \nu x + b_{\nu} \sin \nu x )$$在将三角多项式使用复数表示之前,我们先介绍一下欧拉公式,它是复分析领域的公式,它将三角函数与复指数函数关联起来,先前一个在复平面的复点只能用笛卡尔坐标系描述,欧拉公式在此提供复点至极坐标的变换。因此需要使用复平面来分析三角级数,因为笛卡尔坐标系(平面直角坐标系)的分析已不能满足需求,必须引入复数。欧拉公式在数学、物理和工程领域应用广泛。
$$e^{ix}=\cos x + i\sin x \qquad ①$$其中 \(e\) 是自然对数的底数,\(i\) 是虚数单位,而 \(\cos\) 和 \(\sin\)则是余弦、正弦对应的三角函数,参数 \(x\) 则以弧度为单位。这公式可以说明当 \(x\) 为实数时,函数 \(e^{ix}\) 可在复数平面描述一单位圆。且 \(x\) 为此平面上一条连至原点的线与正实轴的交角。先前一个在复平面的复点只能用笛卡尔坐标系描述,欧拉公式在此提供复点至极坐标的变换。如下图所示:任何复数皆可记为:
$$z=x+yi$$$$z=x+yi=|z|(\cos \theta + i \sin \theta)=|z|e^{i\theta}$$$$z=x-yi=|z|(\cos \theta - i \sin \theta)=|z|e^{-i\theta}$$其中\(z=\sqrt{x^2+y^2}\)为模 ,\(x=Re\{z\}\)为实部,\(y=Im\{z\}\)为虚部。根据欧拉公式,我们还可以得到:$$e^{-ix}=\cos x - i\sin x \qquad ②$$公式①+②可求得到\(\cos x\):$$e^{ix}+e^{-ix}=\cos x + i\sin x + \cos x - i\sin x$$$$\cos x = \frac{1}{2}(e^{ix}+e^{-ix})$$公式①-②可求得到\(\sin x\):$$e^{ix}-e^{-ix}=\cos x + i\sin x - \cos x + i\sin x$$$$\sin x = \frac{1}{2i}(e^{ix}-e^{-ix})$$因为虚数单位\(i^2=-1\),所以$$\sin x = -\frac{1}{2}i(e^{ix}-e^{-ix})$$我们把\(n\)阶的傅里叶级数展开,可得到:$$f(x)=\frac{1}{2}a_0 + a_1\cos 1x + b_1\sin 1x + a_2\cos 2x + b_2\sin 2x + $$$$a_3\cos 3x + b_3\sin3x+\cdots+a_{\nu}\cos \nu x + b_{\nu} \sin \nu x$$使用\(\cos \nu x = \frac{1}{2}(e^{i\nu x}+e^{-i \nu x}), \sin \nu x = -\frac{1}{2}i(e^{i\nu x} - e^{-i \nu x})\)进行代换,得到:$$f(x)=\frac{1}{2}a_0+a_1\frac{1}{2}(e^{i1x}+e^{-i1x})-b_1\frac{1}{2}i(e^{i1x}-e^{-i1x})$$$$+a_2\frac{1}{2}(e^{i2x}+e^{-i2x})-b_2\frac{1}{2}i(e^{i2x}-e^{-i2x})$$$$+a_3\frac{1}{2}(e^{i3x}+e^{-i3x})-b_3\frac{1}{2}i(e^{i3x}-e^{-i3x})+\cdots$$$$+a_{\nu}\frac{1}{2}(e^{i\nu x}+e^{-i\nu x})-b_{\nu}\frac{1}{2}i(e^{i\nu x}-e^{-i\nu x})$$再展开,得到:$$f(x)=\frac{1}{2}a_0+a_1\frac{1}{2}e^{i1x}+a_1\frac{1}{2}e^{-i1x}-b_1\frac{1}{2}ie^{i1x}+b_1\frac{1}{2}ie^{-i1x}$$$$+a_2\frac{1}{2}e^{i2x}+a_2\frac{1}{2}e^{-i2x}-b_2\frac{1}{2}ie^{i2x}+b_2\frac{1}{2}ie^{-i2x}$$$$+a_3\frac{1}{2}e^{i3x}+a_3\frac{1}{2}e^{-i3x}-b_3\frac{1}{2}ie^{i3x}+b_3\frac{1}{2}ie^{-i3x}+\cdots+$$$$+a_{\nu}\frac{1}{2}e^{i\nu x}+a_{\nu}\frac{1}{2}e^{-i\nu x}-b_{\nu}\frac{1}{2}ie^{i\nu x}+b_{\nu}\frac{1}{2}ie^{-i\nu x}$$合并\(e^{i\nu x},e^{-i \nu x}\)项:$$f(x)=\frac{1}{2}a_0 + \frac{1}{2}(a_1 - ib_1)e^{i1x} + \frac{1}{2}(a_1+ib_1)e^{-i1x}$$$$+ \frac{1}{2}(a_2 - ib_2)e^{i2x} + \frac{1}{2}(a_2+ib_2)e^{-i2x}+$$$$+ \frac{1}{2}(a_3 - ib_3)e^{i3x} + \frac{1}{2}(a_3+ib_3)e^{-i3x}+\cdots$$$$+ \frac{1}{2}(a_{\nu} - ib_{\nu})e^{i\nu x} + \frac{1}{2}(a_{\nu}+ib_{\nu})e^{-i\nu x}$$综上所述,多项式共有\(2\nu +1\)个项目,其中\(\nu\)项对应\(-\nu \)项, 所以可以将上述多项式使用和式$$f(x)=\sum_{\nu=-n}^n a_{\nu}e^{i\nu x}$$其中复数\(a_{\nu}\)按照等式 $$\ \begin{cases} a_{\nu}=\frac{1}{2}(a_{\nu} - ib_{\nu}) & ① \\ a_{-\nu}=\frac{1}{2}(a_{\nu} + ib_{\nu}),& 对于 \nu=1,2,\cdots n, ②\\ a_0=\frac{1}{2}a_0 \end{cases}\$$对于上述表达式,使用①+②和①-②,可得到:$$\ \begin{cases} a_{\nu} = a_{\nu} + a_{-\nu} \\ b_{\nu} = i( a_{\nu} - a_{-\nu}) \impliedby a_{\nu}-a_{-\nu}=-ib_{\nu} \\ \end{cases}\$$我们可以把形如:$$f(x)=\sum_{\nu=-n}^n a_{\nu}e^{i\nu x}$$的任何表达式看作一个表示振动的叠加函数,这些振动都写成了复数的形式,当且仅当\(a_{\nu}+a_{-\nu}\)是实的且\(a_{\nu} - a_{-\nu}\)是纯虚的时,也就是\(a_{\nu}和a_{-\nu}\)是共轭复数时,这一叠加的结果才是实的。一个复函数\(\gamma(x)=p(x) + iq(x)\),其积分由下式定义$$\int \gamma(x)dx=\int p(x)dx + i\int q(x)dx$$因此对于\(n \neq 0 \)有$$\int e^{inx} = \int \cos nxdx + i \int \sin nx dx$$$$=\frac{1}{n}\sin nx - \frac{i}{n} \cos nx = \frac{1}{in}e^{inx}$$上式的推导过程是,将两个表达式的分子分母同时乘以\(i\)得到:$$=\frac{1}{n}\sin nx - \frac{i}{n} \cos nx = \frac{1}{in}i\sin nx - \frac{i^2}{in} \cos nx$$$$\frac{1}{in}i\sin nx + \frac{1}{in} \cos nx=\frac{1}{in}(\cos nx + i\sin nx)$$使用同样的推导,我们可计算得到:$$\int e^{-inx}=-\frac{1}{in}e^{-inx}$$特别地,对于任意整数(n)我们有
$$
\ \int_{\pi}^{\pi}e^{inx}dx =
\begin{cases}
0, & 当 n \neq 0 \
2\pi, & 当n=0
\end{cases}
$$
更一般地,如果我们记住(e^{inx}e^{-imx}=e^{i(n-m)x}),就可对于任何整数(m,n),我们有:
$$
\ \int_{\pi}^{\pi}e^{inx}e^{-inx}dx =
\begin{cases}
0, & 当 n \neq m, \
2\pi, & 当 n=m.
\end{cases}
$$
我们把傅里叶复数表达式$$f(x)=\sum_{\nu=-n}^n a_{\nu}e^{i\nu x}$$两边同时乘以\(e^{-i\nu x} (\nu \neq 0)\),并展开得:$$f(x)e^{-i\nu x} = a_{-n}e^{-inx}e^{-ivx}+a_{-(n-1)}e^{-i(n-1)x}e^{-ivx}$$$$+a_{-(n-2)}e^{-i(n - 2)x}e^{-ivx}+\cdots + $$$$+a_1e^{i1x}e^{-ivx}+a_2e^{i2x}e^{-ivx}+\cdots+a_ne^{inx}e^{-ivx}$$两边同时积分,根据上面关于三角函数复数的正交特性,所有\(n \neq \nu\)项的积分等于零,所以$$\int_{-\pi}^{\pi} f(x)e^{-i\nu x}dx = a_{-\nu}\int_{-\pi}^{\pi} e^{-i\nu x } e ^{-i\nu x} =a_{-\nu}2\pi$$$$a_{-\nu}=\frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)e^{-i\nu x}dx$$因\(a_{\nu} = a_{\nu} + a_{-\nu}\),上式中\(a_{\nu}=0\),故$$a_{\nu}=\frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)e^{-i\nu x}dx$$使用复数计算下面函数的傅里叶的展开式
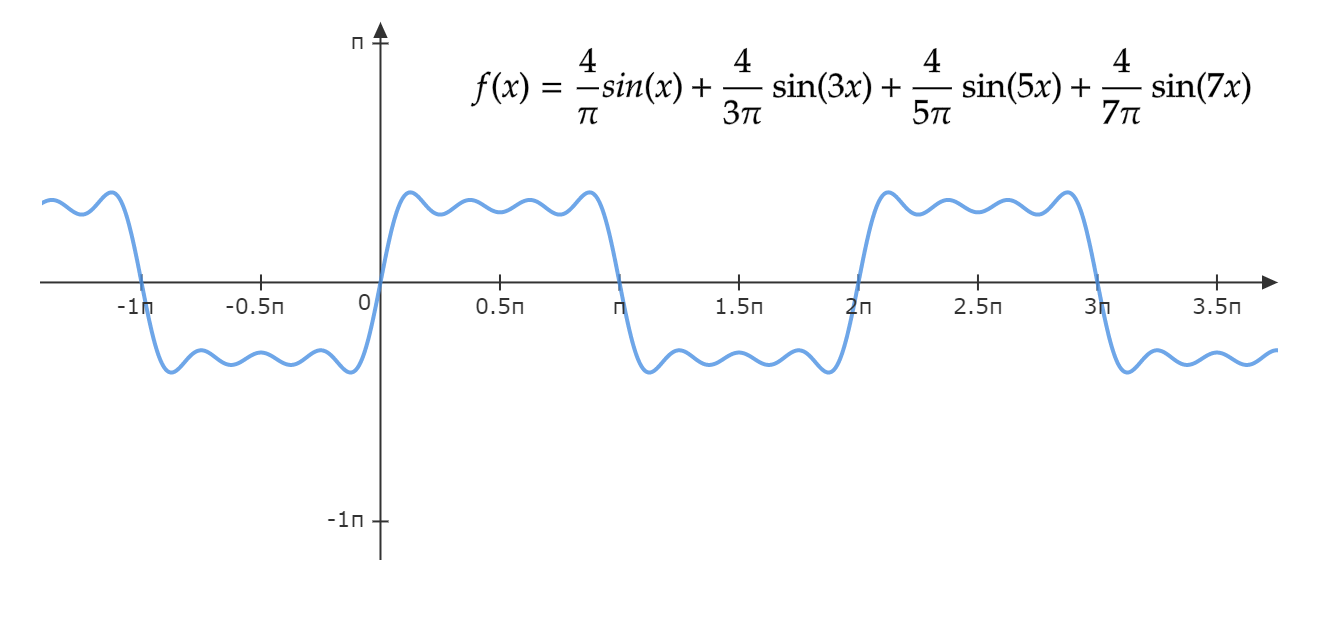
$$\ f(x)=sign x = \begin{cases} -1, & -\pi \leq x \leq 0\\ 1, & 0 < x \leq \pi \end{cases}\
$$该函数的图像如下:
下面是该多项式前4项的拟合图像