在函数的极值和最值中讨论的是无条件极值，对自变量没有作限制。如果对自变量作一定的限制，则相应的极值问题就是条件极值问题。在函数的极值和最值文章中计算无盖长方形水箱，当水箱的长、宽、高各取多大，才能是用料最省的例子中，它的约束条件就是

$$ xyz = V $$ 当有这个约束条件时，$x,y,z$其中之一取零是没有意义的。

一般的条件极值的提法

求目标函数 $$ z=f(x,y) $$ 在约束条件 $$ \varphi(x,y) = 0 $$ 下的极值。

条件极值的几何解释

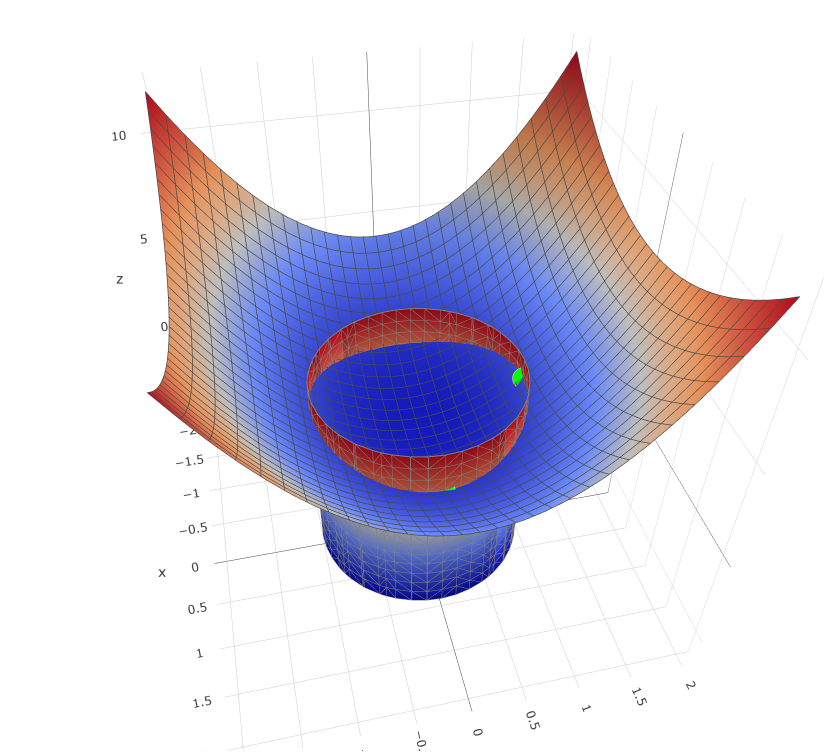
假设有一个二元函数它的图像如下图所示：

$/assets/images/article/math/e00dc5e1-75ee-4e9e-9773-b880e617156a$

该函数在$ (x_1, y_1)$处取得一个无条件的极大值$f(x_1, y_1)$。当增加一个条件函数时 $$ \varphi(x,y)= 0 $$ 它在平面上表现为一条曲线，那么在这条曲线上的点，哪一点的函数值最大？通过上图可知，以曲线$\varphi(x,y)$为准线，作平行$z$轴的柱面，该柱面与曲面$z=f(x,y)$有一条交线，那么该交线的最高点在$(x_0, y_0)$处。

条件极值的必要条件

先看一个图形

$/assets/images/article/math/6f9a8644-20e4-4e88-8c1a-f1c0521ccb26$

函数$f(x,y)$在哪里取得条件最大值？从图像可以看出，当函数$\varphi(x,y)=0$与等值线$f(x,y)=c(c为常数)$相切时，取得最大值。
设$z_0=f(x_0, y_0)$是$z=f(x,y)$在条件$\varphi(x,y)=0$下的极值，现假设二元函数$\varphi(x,y)=0$确定了一个一元隐函数$y=y(x)$，将该函数代入到$z=f(x,y)$得到一个一元函数 $$ z=f(x,y(x)) $$ 该函数在$x=x_0$处取得极值。为了求得极值点，我们可以利用一元函数极值的必要条件。求导并令导数等于零。 $$ \frac{dz}{dx}=f_x \cdot 1 + f_y \cdot \frac{dy}{dx} = 0 $$ 代入$(x_0, y_0)$得到： $$ f_x(x_0, y_0) + f_y(x_0, y_0)\cdot y\,'(x_0) = 0 $$ 那么，我们可以求得函数$y=y(x)$在$x_0$处的导数 $$ y\,'(x_0) = -\frac{f_x(x_0, y_0)}{f_y(x_0, y_0)} $$ 另一方面，由隐函数的求导法则可知，隐函数$\varphi(x,y)= 0$的导数 $$ \frac{dy}{dx} = y\,'(x_0)=-\frac{\varphi_x(x_0, y_0)}{\varphi_y(x_0, y_0)} $$ 因此，可以得到 $$ \frac{f_x(x_0, y_0)}{f_y(x_0, y_0)} = \frac{\varphi_x(x_0, y_0)}{\varphi_y(x_0, y_0)} $$ 通过对上式进行变换，得到： $$ \frac{f_x(x_0, y_0)}{\varphi_x(x_0, y_0)} = \frac{f_y(x_0, y_0)}{\varphi_y(x_0, y_0)} $$ 因为两个向量平行的条件是对应的分量成比例，所以对于上述公式我们可以理解为两个向量平行。 $$ \Big(f_x(x_0, y_0), f_y(x_0, y_0)\Big) \parallel \Big(\varphi_x(x_0, y_0), \varphi_y(x_0, y_0)\Big) $$ 或它们的梯度平行 $$ \bigtriangledown f(x_0, y_0) \parallel \bigtriangledown \varphi(x_0, y_0) $$ 它的几何解释是：$\bigtriangledown f(x_0, y_0)$是等值线$f(x,y)=z_0$在点$(x_0, y_0)$处的法向量，$ \bigtriangledown \varphi(x_0, y_0)$是曲线$\varphi(x,y)=0$在点$(x_0, y_0)$处的法向量，两个法向量平行，说明在该点处，它们有相同的切线。所以曲线$\varphi(x,y)=0$在点$(x_0, y_0)$与函数$z=f(x,y)$的等值线$f(x,y)=z_0$相切。
由于两个向量平行，那么存在一个$\lambda$，使得 $$ \bigtriangledown f(x_0, y_0) = -\lambda \bigtriangledown \varphi(x_0, y_0) $$ 这里的$\lambda_0$使用负数，为方便移项后变成正数。 $$ \bigtriangledown f(x_0, y_0) + \lambda \bigtriangledown \varphi(x_0, y_0) = 0 $$ 或 $$ \bigtriangledown(f + \lambda \varphi) = 0 $$ 由上述公式可知，条件极值点就是新的函数的驻点，它们的偏导数等于零。新的函数是 $$ F(x,y, \lambda) = f(x,y) + \lambda\varphi(x,y) $$ 则 $$ \bigtriangledown F(x_0, y_0, \lambda) = 0 $$ 即 $(x_0, y_0, \lambda)$是函数$F(x,y, \lambda)$的驻点。新函数 $$ F(x,y, \lambda) = f(x,y) + \lambda\varphi(x,y) $$ 称为拉格朗日函数，其中$\lambda$称为拉格朗日乘数。

求条件极值的拉格朗日乘数法

求函数$z=f(x,y)$在条件$\varphi(x,y)=0$下的极值Lagrange乘数法步骤：
1.作lagrange函数： $$ F(x,y, \lambda) = f(x,y) + \lambda \varphi(x,y) $$ 2. 求$F(x,y, \lambda)$的驻点, ，令函数的偏导数等于零。 $$ F_x = f_x(x,y) + \lambda \varphi_x(x,y) = 0 $$ $$ F_y = f_y(x,y) + \lambda \varphi_y(x,y) = 0 $$ $$ F_{\lambda} = \varphi_x(x,y) = 0 $$ 解以上方程组，得到驻点$(x_0, y_0, \lambda_0)$
3. $(x_0, y_0)$便可能是条件极值点

Lagrange乘数法的思路是：利用Lagrange乘数，将目标函数（二元函数）与约束条件结合在一起构造出Lagrange函数（三元函数），从而将二元函数的条件极值问题，转化为三元函数的无条件极值问题。

例

例1

目标函数$z = xy$,约束条件$x+y=1$

解

作Lagrange函数 $$ F(x,y, \lambda)=xy + \lambda(x+y-1) $$ 求$F$的驻点 $$ F_x = y + \lambda = 0 $$ $$ F_y = x + \lambda = 0 $$ $$ F_{\lambda} = x+y-1 = 0 $$ 解方程组得： $$ x = \frac{1}{2}, \quad y = \frac{1}{2}, \quad \lambda = -\frac{1}{2} $$ 故$(\frac{1}{2}, \frac{1}{2})$就是可能的条件极值点。条件极值 $$ z=z(\frac{1}{2},\frac{1}{2}) = \frac{1}{4} $$

该函数的图像如下：

$/assets/images/article/math/e11bedfe-a41f-40b0-a5e6-33f537f98ebd$

例2

求函数$z=x^2+2y^2$在圆周$x^2+y^2=1$上的极值

解

作Lagrange函数： $$ F(x, y, \lambda) = f(x,y) + \lambda \varphi(x,y) = x^2+2y^2 + \lambda(x^2+y^2-1) $$ 求$F$驻点 $$ F_x = 2x + 2\lambda x = 0 $$ $$ F_y=4y + 2\lambda y = 0 $$ $$ F_{\lambda}=x^2+y^2-1 = 0 $$ 解方程得到 $$ x = 0, y=\pm 1, \quad y=0, x=\pm 1 $$ 因此，有四个驻点$(0, 1), (0, -1), (1, 0), (-1, 0)$。 $$ z(0,1) = 2, \quad z(0,-1) = 2, \quad z(1,0)=1, \quad z(-1,0)=1。 $$ 该函数如下图所示

$/assets/images/article/math/b0e8340b-12c7-438c-bafe-586c728feab4$

$/assets/images/article/math/c318f60b-1d53-4300-a2fc-9117b6384bc0$

例3

在多元函数的极值和最值的文章中，使用Lagrange乘数法解其中立方体最省料的例子。

求函数$S = xy + 2(xz + yz)$的最小值。在约束条件$V=xyz$下的极小值

解

作Lagrange函数： $$ F(x,y,z,V) = xy + 2(xz+yz) + \lambda(xyz - V) $$ 求$F$的驻点，令偏导数为零。 $$ F_x = y+2z+\lambda yz=0 \quad (1) $$ $$ F_y = x + 2z + \lambda xz = 0 \quad (2) $$ $$ F_z = 2x + 2y + \lambda xy = 0 \quad (3) $$ $$ F_{\lambda}=xyz-V=0 \quad (4) $$ 解上面的方程组，$(1)-(2)$得到： $$ (y-x) + \lambda z(y-x) = 0 \implies x = y $$ 代入$(3)$得到 $\lambda x = -4$，再代入$(2)$得到 $z=\frac{1}{2}x$,再代入$(4)$得到: $$ \frac{1}{2}x^3 -V= 0 \implies x = \sqrt[3]{2V}, z = \frac{\sqrt[3]{2V}}{2} $$ 它与函数的极值和最值中计算的结果一致。

拉格朗日乘数法的推广

拉格朗日乘数法可推广到有多个约束条件的条件极值问题

求三元函数
$$
u=f(x,y,z)
$$
在两个约束条件
$$
G(x,y,z) = 0, \quad H(x,y,z) = 0
$$
下的极值，它的几何意义就是在这两个曲面上的交线上变动时，求相应的函数的极值。它的Lagrange函数是
$$
F(x,y,z, \lambda, \mu) = f(x,y,z) + \lambda G(x,y,z) + \mu H(x,y,z)
$$

例

抛物面$z=x^2+y^2$被平面$x+y+z=1$截成一椭圆，求这椭圆上的点到原点的距离的最大值与最小值。

解

设椭圆上的任意点为$(x,y,z)$,则椭圆上的点到原点的距离有以下式子： $$ d^2=x^2+y^2+z^2 $$ $x,y,z$满足条件： $$ z=x^2+y^2, \quad x+y+z=1. $$ 作拉格朗日函数： $$ L = x^2+y^2+z^2 + \lambda (z-x^2-y^2) + \mu (x+y+z-1) $$ 分别求偏导数，并令其等于零： $$ L_x = 2x - 2\lambda x + \mu = 0. \quad (1) $$ $$ L_y = 2y - 2 \lambda y + \mu = 0. \quad (2) $$ $$ L_z = 2z + \lambda + \mu = 0. \quad (3) $$ $(1)-(2)$得： $$ (1-\lambda)(x-y) = 0 $$ 故有$\lambda=1$和$x=y$，由$\lambda = 1$，代入$(1)$得到$\mu=0$，将$\mu=0$代入$(3)$得到$z=-\frac{1}{2}$，根据条件函数可知，$z \geq 0$,所以不合题意，故舍去。
将$x=y$代入$z=x^2+y^2$和$x+y+z=1$，得到： $$ 2x^2+2x - 1 = 0 $$ 根据求根公式 $$ ax^2+bx+c = 0 , \quad \ x = \frac{-b + \sqrt{\Delta}}{2a}, \quad \Delta = b^2-4ac $$ 得到： $$ x=y=\frac{-1\pm\sqrt{3}}{2}, \quad z=1-2x = 1 - (-1 \pm \sqrt{3})=2 \pm \sqrt{3} $$ 于是得到两个可能得极值点 $$ M_1(\frac{-1+\sqrt{3}}{2},\frac{-1+\sqrt{3}}{2}, 2-\sqrt{3}), \quad M_2(\frac{-1-\sqrt{3}}{2},\frac{-1-\sqrt{3}}{2}, 2+\sqrt{3}) $$ 由题意可知这中距离得最大值和最小值一定存在。因为$d^2=x^2+y^2+z^2.$所以极值距离是： $$ 2(\frac{-1\pm \sqrt{3}}{2})^2 + (2\pm \sqrt{3})^2=9\pm 5 \sqrt{3} $$

目录

拉格朗日乘数法与条件极值

一般的条件极值的提法

条件极值的几何解释

条件极值的必要条件

求条件极值的拉格朗日乘数法

例

例1

解

例2

解

例3

解

拉格朗日乘数法的推广

例

解